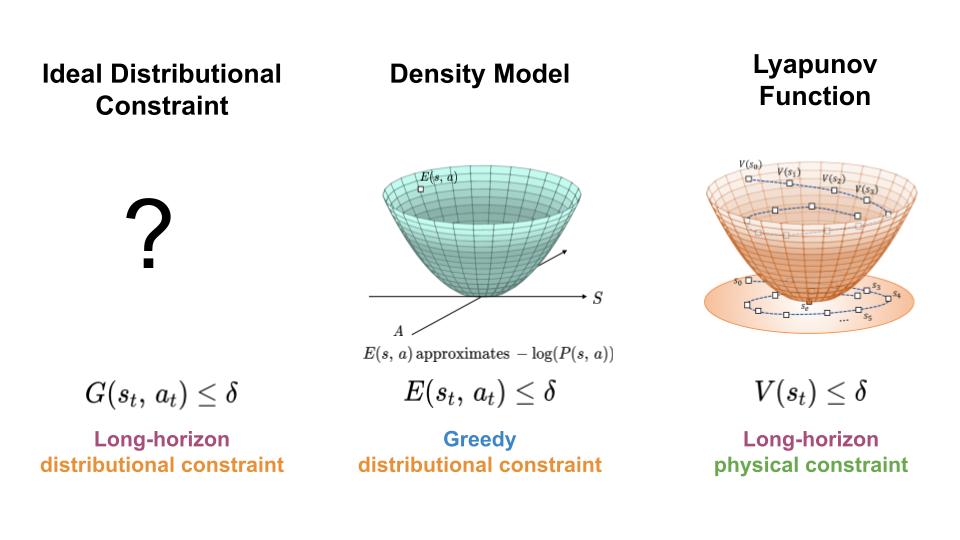
To regulate the distribution shift experience by learning-based controllers, we seek a mechanism for constraining the agent to regions of high data density throughout its trajectory (left). Here, we present an approach which achieves this goal by combining features of density models (middle) and Lyapunov functions (right).
In order to make use of machine learning and reinforcement learning in controlling real world systems, we must design algorithms which not only achieve good performance, but also interact with the system in a safe and reliable manner. Most prior work on safety-critical control focuses on maintaining the safety of the physical system, e.g. avoiding falling over for legged robots, or colliding into obstacles for autonomous vehicles. However, for learning-based controllers, there is another source of safety concern: because machine learning models are only optimized to output correct predictions on the training data, they are prone to outputting erroneous predictions when evaluated on out-of-distribution inputs. Thus, if an agent visits a state or takes an action that is very different from those in the training data, a learning-enabled controller may “exploit” the inaccuracies in its learned component and output actions that are suboptimal or even dangerous.
Continue
Deep neural networks have enabled technological wonders ranging from voice recognition to machine transition to protein engineering, but their design and application is nonetheless notoriously unprincipled.
The development of tools and methods to guide this process is one of the grand challenges of deep learning theory.
In Reverse Engineering the Neural Tangent Kernel, we propose a paradigm for bringing some principle to the art of architecture design using recent theoretical breakthroughs: first design a good kernel function – often a much easier task – and then “reverse-engineer” a net-kernel equivalence to translate the chosen kernel into a neural network.
Our main theoretical result enables the design of activation functions from first principles, and we use it to create one activation function that mimics deep \(\textrm{ReLU}\) network performance with just one hidden layer and another that soundly outperforms deep \(\textrm{ReLU}\) networks on a synthetic task.
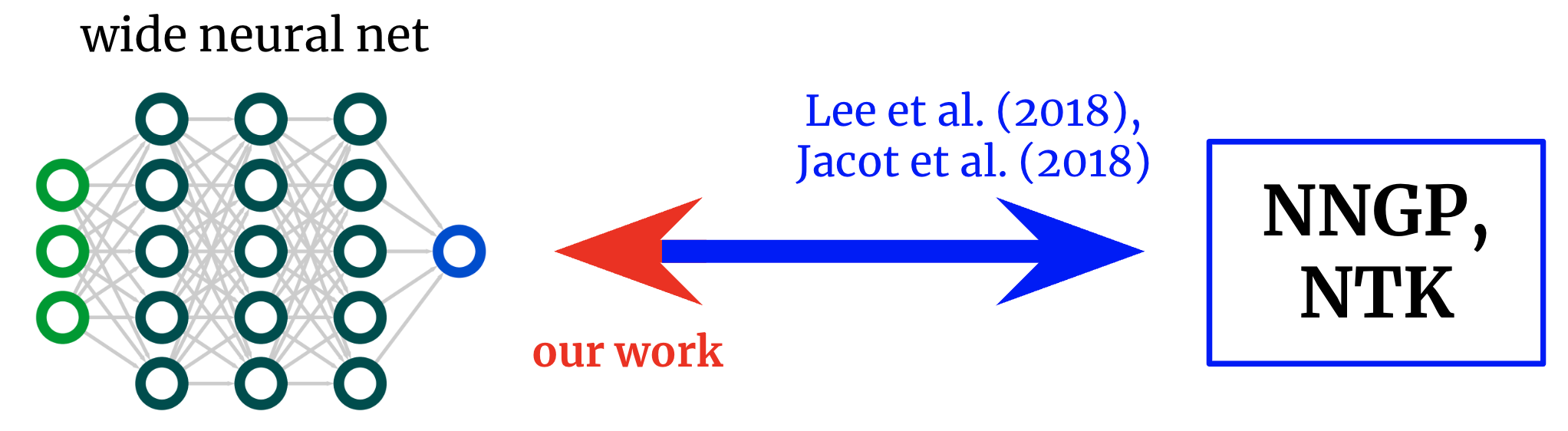
Kernels back to networks. Foundational works derived formulae that map from wide neural networks to their corresponding kernels. We obtain an inverse mapping, permitting us to start from a desired kernel and turn it back into a network architecture.
Continue
Wei Fu, Chao Yu, Zelai Xu, Jiaqi Yang, Yi Wu
Jul 10, 2022
In cooperative multi-agent reinforcement learning (MARL), due to its on-policy nature, policy gradient (PG) methods are typically believed to be less sample efficient than value decomposition (VD) methods, which are off-policy. However, some recent empirical studies demonstrate that with proper input representation and hyper-parameter tuning, multi-agent PG can achieve surprisingly strong performance compared to off-policy VD methods.
Why could PG methods work so well? In this post, we will present concrete analysis to show that in certain scenarios, e.g., environments with a highly multi-modal reward landscape, VD can be problematic and lead to undesired outcomes. By contrast, PG methods with individual policies can converge to an optimal policy in these cases. In addition, PG methods with auto-regressive (AR) policies can learn multi-modal policies.
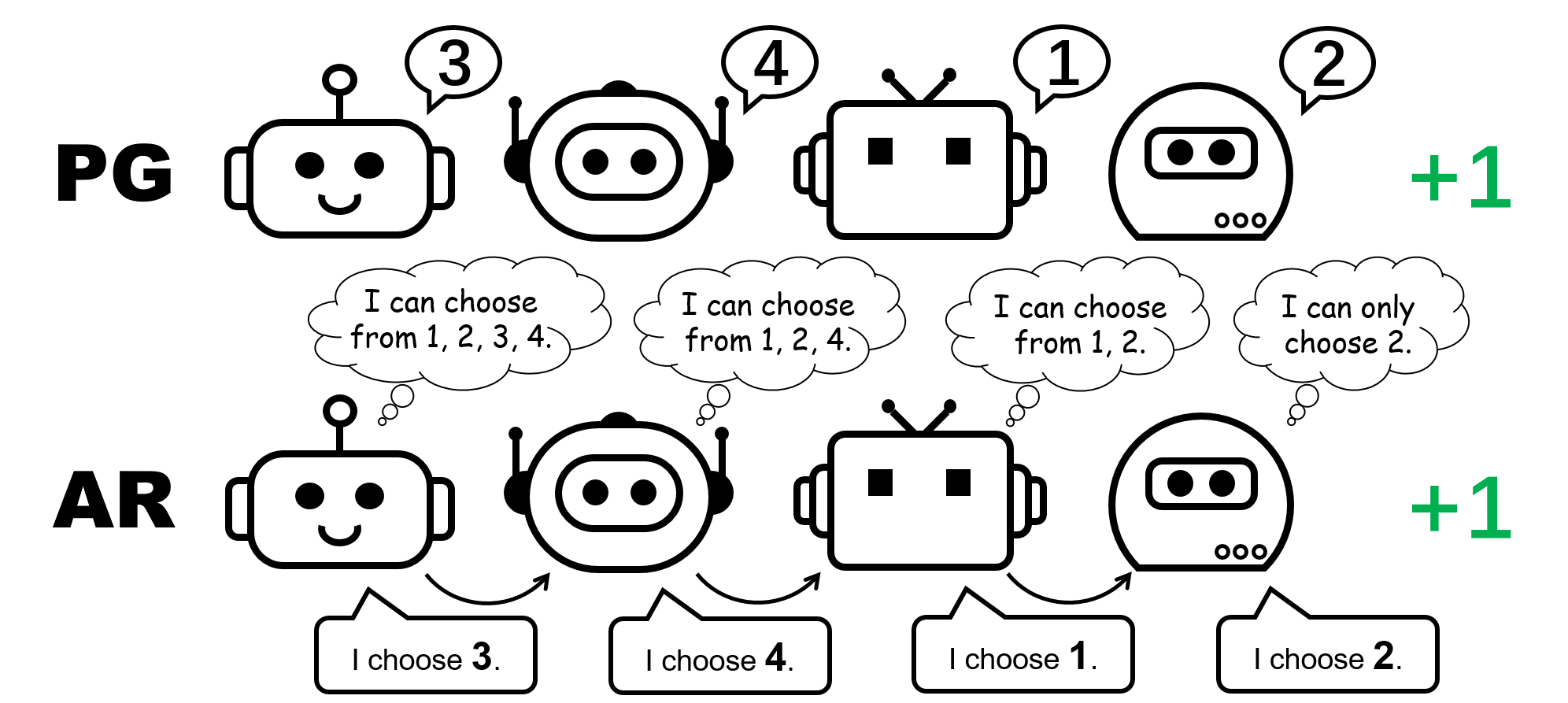
Figure 1: different policy representation for the 4-player permutation game.
Continue

FIGS (Fast Interpretable Greedy-tree Sums): A method for building interpretable models by simultaneously growing an ensemble of decision trees in competition with one another.
Recent machine-learning advances have led to increasingly complex predictive models, often at the cost of interpretability. We often need interpretability, particularly in high-stakes applications such as in clinical decision-making; interpretable models help with all kinds of things, such as identifying errors, leveraging domain knowledge, and making speedy predictions.
In this blog post we’ll cover FIGS, a new method for fitting an interpretable model that takes the form of a sum of trees. Real-world experiments and theoretical results show that FIGS can effectively adapt to a wide range of structure in data, achieving state-of-the-art performance in several settings, all without sacrificing interpretability.
Continue
We recently published the Berkeley Crossword Solver (BCS), the current state of the art for solving American-style crossword puzzles. The BCS combines neural question answering and probabilistic inference to achieve near-perfect performance on most American-style crossword puzzles, like the one shown below:

Figure 1: Example American-style crossword puzzle
An earlier version of the BCS, in conjunction with Dr.Fill, was the first computer program to outscore all human competitors in the world’s top crossword tournament. The most recent version is the current top-performing system on crossword puzzles from The New York Times, achieving 99.7% letter accuracy (see the technical paper, web demo, and code release).
Continue
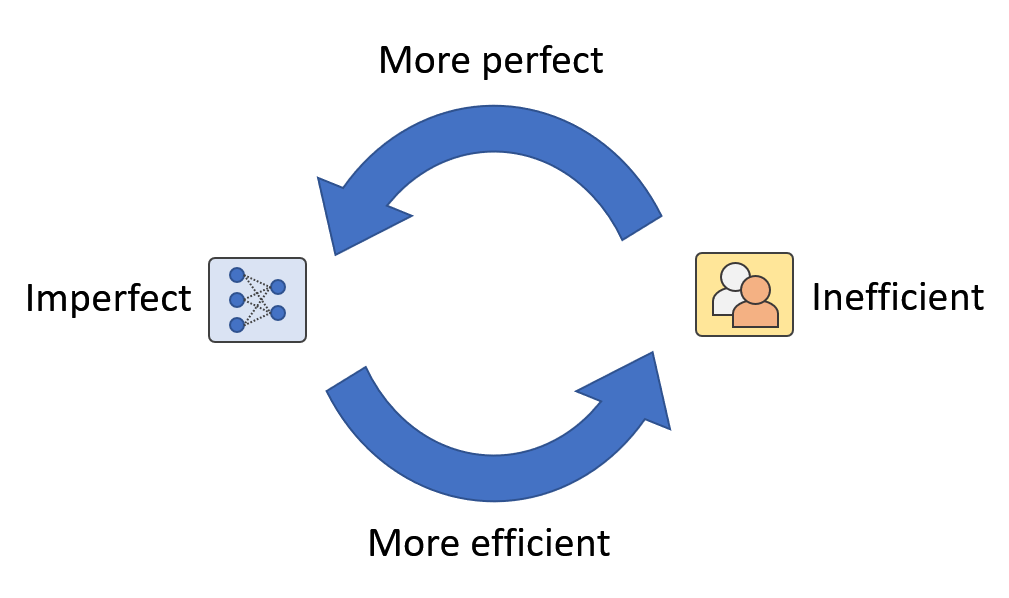
Figure 1: In real-world applications, we think there exist a human-machine loop where humans and machines are mutually augmenting each other. We call it Artificial Augmented Intelligence.
How do we build and evaluate an AI system for real-world applications? In most AI research, the evaluation of AI methods involves a training-validation-testing process. The experiments usually stop when the models have good testing performance on the reported datasets because real-world data distribution is assumed to be modeled by the validation and testing data. However, real-world applications are usually more complicated than a single training-validation-testing process. The biggest difference is the ever-changing data. For example, wildlife datasets change in class composition all the time because of animal invasion, re-introduction, re-colonization, and seasonal animal movements. A model trained, validated, and tested on existing datasets can easily be broken when newly collected data contain novel species. Fortunately, we have out-of-distribution detection methods that can help us detect samples of novel species. However, when we want to expand the recognition capacity (i.e., being able to recognize novel species in the future), the best we can do is fine-tuning the models with new ground-truthed annotations. In other words, we need to incorporate human effort/annotations regardless of how the models perform on previous testing sets.
Continue
Deep reinforcement learning (DRL) is transitioning from a research field focused on game playing to a technology with real-world applications. Notable examples include DeepMind’s work on controlling a nuclear reactor or on improving Youtube video compression, or Tesla attempting to use a method inspired by MuZero for autonomous vehicle behavior planning. But the exciting potential for real world applications of RL should also come with a healthy dose of caution - for example RL policies are well known to be vulnerable to exploitation, and methods for safe and robust policy development are an active area of research.
At the same time as the emergence of powerful RL systems in the real world, the public and researchers are expressing an increased appetite for fair, aligned, and safe machine learning systems. The focus of these research efforts to date has been to account for shortcomings of datasets or supervised learning practices that can harm individuals. However the unique ability of RL systems to leverage temporal feedback in learning complicates the types of risks and safety concerns that can arise.
This post expands on our recent whitepaper and research paper, where we aim to illustrate the different modalities harms can take when augmented with the temporal axis of RL. To combat these novel societal risks, we also propose a new kind of documentation for dynamic Machine Learning systems which aims to assess and monitor these risks both before and after deployment.
Continue

Figure 1: Summary of our recommendations for when a practitioner should BC and various imitation learning style methods, and when they should use offline RL approaches.
Offline reinforcement learning allows learning policies from previously collected data, which has profound implications for applying RL in domains where running trial-and-error learning is impractical or dangerous, such as safety-critical settings like autonomous driving or medical treatment planning. In such scenarios, online exploration is simply too risky, but offline RL methods can learn effective policies from logged data collected by humans or heuristically designed controllers. Prior learning-based control methods have also approached learning from existing data as imitation learning: if the data is generally “good enough,” simply copying the behavior in the data can lead to good results, and if it’s not good enough, then filtering or reweighting the data and then copying can work well. Several recent works suggest that this is a viable alternative to modern offline RL methods.
This brings about several questions: when should we use offline RL? Are there fundamental limitations to methods that rely on some form of imitation (BC, conditional BC, filtered BC) that offline RL addresses? While it might be clear that offline RL should enjoy a large advantage over imitation learning when learning from diverse datasets that contain a lot of suboptimal behavior, we will also discuss how even cases that might seem BC-friendly can still allow offline RL to attain significantly better results. Our goal is to help explain when and why you should use each method and provide guidance to practitioners on the benefits of each approach. Figure 1 concisely summarizes our findings and we will discuss each component.
Continue

A demonstration of the RvS policy we learn with just supervised learning and a depth-two MLP. It uses no TD learning, advantage reweighting, or Transformers!
Offline reinforcement learning (RL) is conventionally approached using value-based methods based on temporal difference (TD) learning. However, many recent algorithms reframe RL as a supervised learning problem. These algorithms learn conditional policies by conditioning on goal states (Lynch et al., 2019; Ghosh et al., 2021), reward-to-go (Kumar et al., 2019; Chen et al., 2021), or language descriptions of the task (Lynch and Sermanet, 2021).
We find the simplicity of these methods quite appealing. If supervised learning is enough to solve RL problems, then offline RL could become widely accessible and (relatively) easy to implement. Whereas TD learning must delicately balance an actor policy with an ensemble of critics, these supervised learning methods train just one (conditional) policy, and nothing else!
Continue

Figure 1: Airmass measurements (clouds) over Ukraine from February 18, 2022 - March 01, 2022 from the SEVIRI instrument. Data accessed via the EUMETSAT Viewer.
Satellite imagery is a critical source of information during the current invasion of Ukraine. Military strategists, journalists, and researchers use this imagery to make decisions, unveil violations of international agreements, and inform the public of the stark realities of war. With Ukraine experiencing a large amount of cloud cover and attacks often occuring during night-time, many forms of satellite imagery are hindered from seeing the ground. Synthetic Aperture Radar (SAR) imagery penetrates cloud cover, but requires special training to interpret. Automating this tedious task would enable real-time insights, but current computer vision methods developed on typical RGB imagery do not properly account for the phenomenology of SAR. This leads to suboptimal performance on this critical modality. Improving the access to and availability of SAR-specific methods, codebases, datasets, and pretrained models will benefit intelligence agencies, researchers, and journalists alike during this critical time for Ukraine.
In this post, we present a baseline method and pretrained models that enable the interchangeable use of RGB and SAR for downstream classification, semantic segmentation, and change detection pipelines.
Continue









