Cross-posted from the DeepMind Safety blog.
In many reinforcement learning problems the objective is too complex to be specified procedurally, and a reward function must instead be learned from user data. However, how can you tell if a learned reward function actually captures user preferences? Our method, Equivalent-Policy Invariant Comparison (EPIC), allows one to evaluate a reward function by computing how similar it is to other reward functions. EPIC can be used to benchmark reward learning algorithms by comparing learned reward functions to a ground-truth reward. It can also be used to validate learned reward functions prior to deployment, by comparing them against reward functions learned via different techniques or data sources.
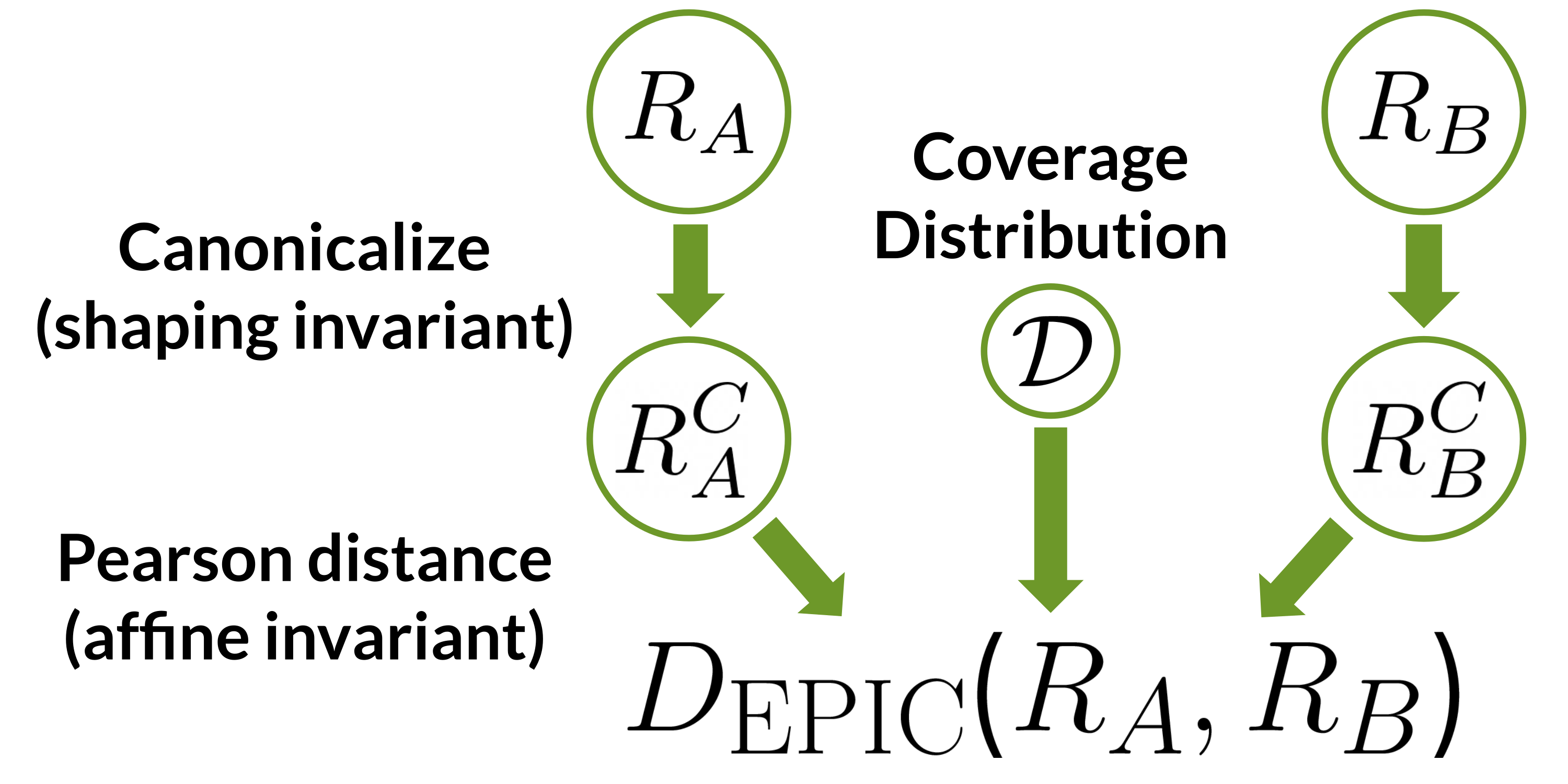
Figure 1: EPIC compares reward functions $R_a$ and $R_b$ by first mapping them to canonical representatives and then computing the Pearson distance between the canonical representatives on a coverage distribution $\mathcal{D}$. Canonicalization removes the effect of potential shaping, and Pearson distance is invariant to positive affine transformations.
EPIC is up to 1000 times faster than alternative evaluation methods, and requires little to no hyperparameter tuning. Moreover, we show both theoretically and empirically that reward functions judged as similar by EPIC induce policies with similar returns, even in unseen environments.
Introducing EPIC
Specifying a reward function can be one of the trickiest parts of applying RL to a problem. Even seemingly simple robotics tasks such as peg insertion can require first training an image classifier to use as a reward signal. Tasks with a more nebulous objective like article summarization require collecting large amounts of human feedback in order to learn a reward function. The difficulty of reward function specification will only continue to grow as RL is increasingly applied to complex and user-facing applications such as recommender systems, chatbots and autonomous vehicles.
Figure 2: There exist a variety of techniques to specify a reward function. EPIC can help you decide which one works best for a given task.
This challenge has led to the development of a variety of methods for specifying reward functions. In addition to hand-designing a reward function, today it is possible to learn a reward function from data as varied as the initial state, demonstrations, corrections, preference comparisons, and many other data sources. Given this dizzying array of possibilities, how should we choose which method to use?
EPIC is a new way to evaluate reward functions and reward learning algorithms by comparing how similar reward functions are to one another. We anticipate two main use cases for EPIC:
- Benchmarking in tasks where the reward function specification problem has already been solved, giving a “ground-truth” reward. We can then compare learned rewards directly to this “ground-truth” to gauge the performance of a new reward learning method.
- Validation of reward functions prior to deployment. In particular, we often have a collection of reward functions specified by different people, methods or data sources. If multiple distinct approaches produce similar reward functions (i.e. a low EPIC distance to one another) then we can have more confidence that the resulting reward is correct. More generally, if two reward functions have low EPIC distance to one another, then information we gain about one (such as by using interpretability methods) also helps us understand the other.
Perhaps surprisingly, there is (to the best of our knowledge) no prior work that focuses on directly comparing reward functions. Instead, most prior work has used RL to train a policy on learned rewards, and then evaluated the resulting policies. Unfortunately, RL training is computationally expensive. Moreover, it is unreliable: if the policy performs poorly, we cannot tell if this is due to the learned reward failing to match user preferences, or the RL algorithm failing to optimize the learned reward.
A more fundamental issue with evaluation based on RL training is that two rewards can induce identical policies in an evaluation environment, yet lead to totally different behavior in the deployment environment. Suppose all states ${X, Y, Z}$ are reachable in the evaluation environment. If the user prefers $X > Y > Z$, but the agent instead learns $X > Z > Y$, the agent will still go to the correct state $X$ during evaluation. But if $X$ is no longer reachable at deployment, the previously reliable agent would misbehave by going to the least-favoured state $Z$.
By contrast, EPIC is fast, reliable and can predict return even in unseen deployment environments. Let’s look at how EPIC is able to achieve this.
Our method, Equivalent-Policy Invariant Comparison (EPIC), works by comparing reward functions directly, without training a policy. It is designed to be invariant to two transformations that never change the optimal policy:
- Potential shaping, which moves reward earlier or later in time.
- Positive affine transformations, adding a constant or rescaling by a positive factor.
EPIC is computed in the two stages illustrated in Figure 1 (above), mirroring these invariants:
- First, we canonicalize the rewards being compared. Rewards that are the same up to potential shaping are mapped to the same canonical representative.
- Next, we compute the Pearson correlation between the canonical representatives, over some coverage distribution $\mathcal{D}$ over transitions. Pearson correlation is invariant to positive affine transformations. Finally, we transform the correlation, a measure of similarity, into a distance.
Why use EPIC?
EPIC satisfies important properties you’d expect from a distance, namely symmetry and the triangle inequality. This gives the distance an intuitive interpretation, and allows it to be used in algorithms that rely on distance functions.
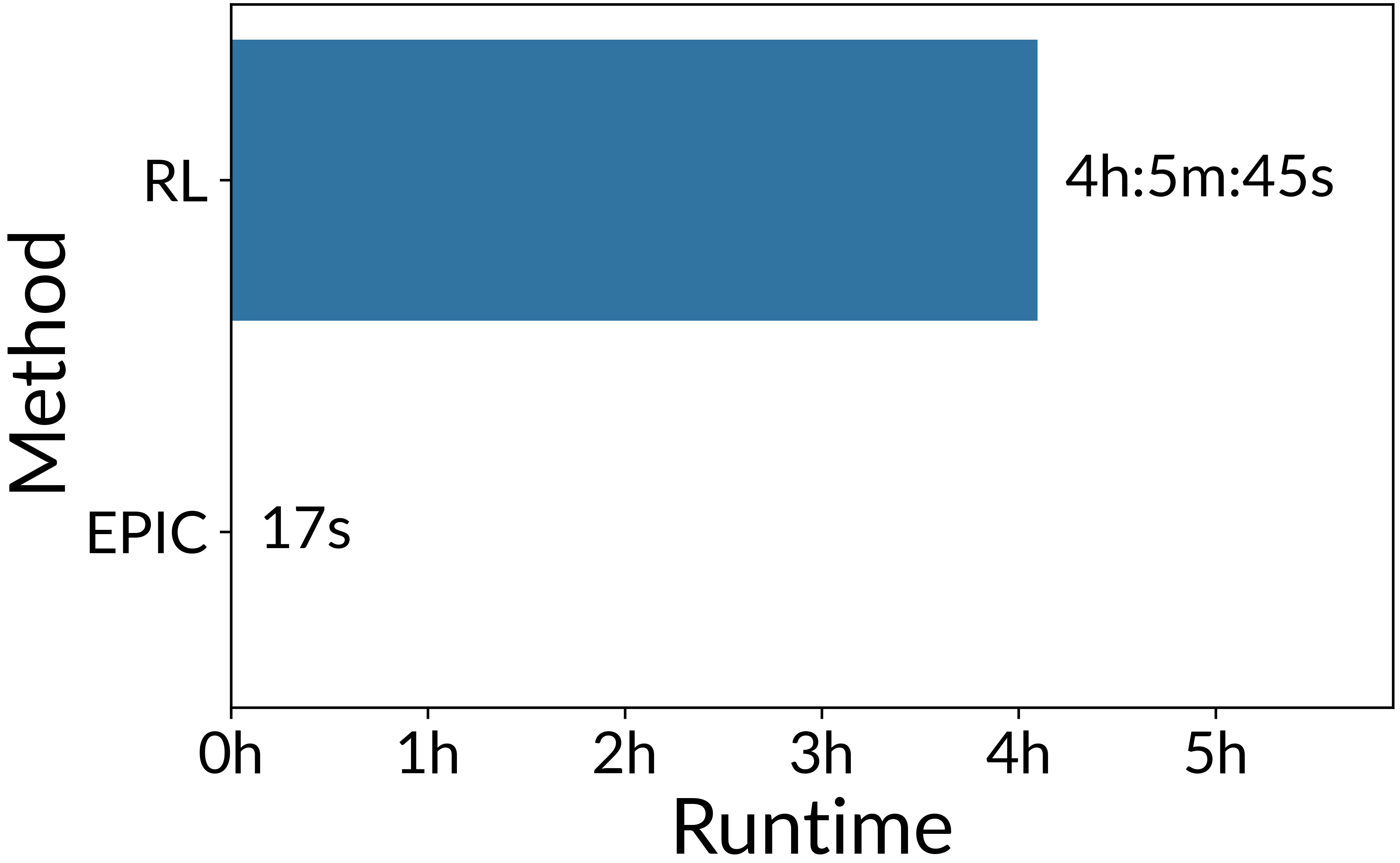
Figure 3: Runtime needed to perform pairwise comparison of 5 reward functions in a simple continuous control task.
Furthermore, EPIC is over 1000 times faster than comparison using RL training when tested in a simple point mass continuous control task. It’s also easy to use: the only hyperparameters that need to be set are the coverage distribution and the number of samples to take.
A key theoretical result is that low EPIC distance predicts similar policy returns. Specifically, EPIC distance bounds the difference in the return G of optimal policies $\pi_A^\ast$ and $\pi_B^\ast$ for rewards $R_A$ and $R_B$ (see Theorem 4.9):
\[G_{R_A}(\pi_A^\ast) - G_{R_A}(\pi_B^\ast) \leq K(\mathcal{D}) ||R_A||_2 D_{EPIC}(R_A, R_B)\]where $K(\mathcal{D})$ is a constant that depends on the support of the EPIC coverage distribution. This bound holds for optimal policies computed in any MDP that has the same state and action spaces as the rewards $R_A$ and $R_B$. In that sense, EPIC gives a much stronger performance guarantee than policy evaluation in a single instance of a task.
However, this result does depend on the distribution $\mathcal{D}$ having adequate coverage over the transitions visited by the optimal policies $\pi_A^\ast$ and $\pi_B^\ast$. In general, we recommend choosing $\mathcal{D}$ to have coverage on all plausible transitions. This ensures adequate support for $\pi_A^\ast$ and $\pi_B^\ast$, without wasting probability mass on physically impossible transitions that will never occur.
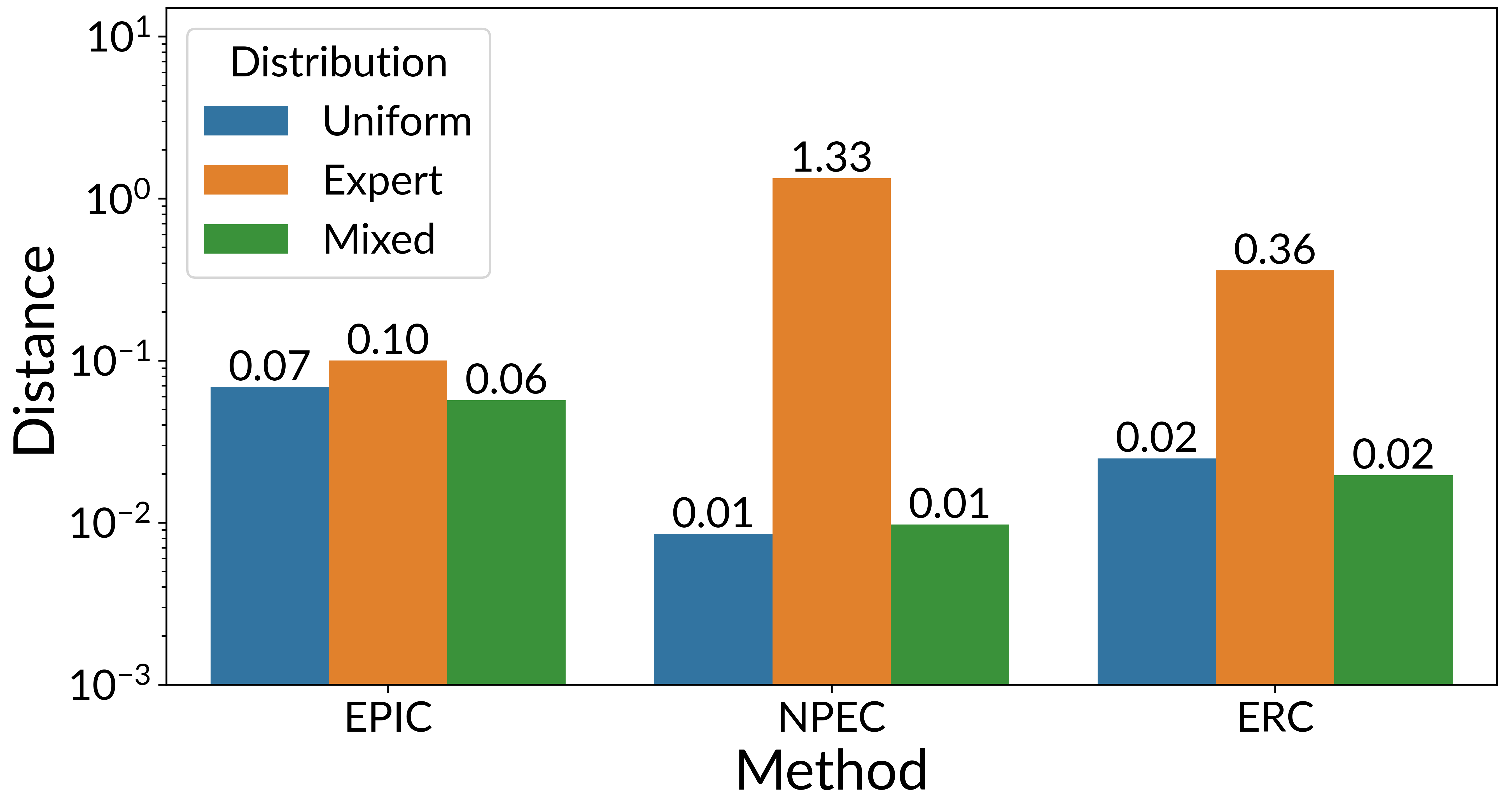
Figure 4:
EPIC distance between rewards is similar across different distributions (colored bars), while baselines (NPEC and ERC) are highly sensitive to distribution. The coverage distribution consists of rollouts from: a policy that takes actions uniformly at random, an expert optimal policy and a mixed policy that randomly transitions between the other two.
While EPIC’s theoretical guarantee is dependent on the coverage distribution $\mathcal{D}$, we find that in practice EPIC is fairly robust to the exact choice of distribution: a variety of reasonable distributions give similar results. The figure above illustrates this: EPIC (left) computes a similar distance under different coverage distributions (colored bars), while baselines NPEC (middle) and ERC (right) exhibit significant variance.
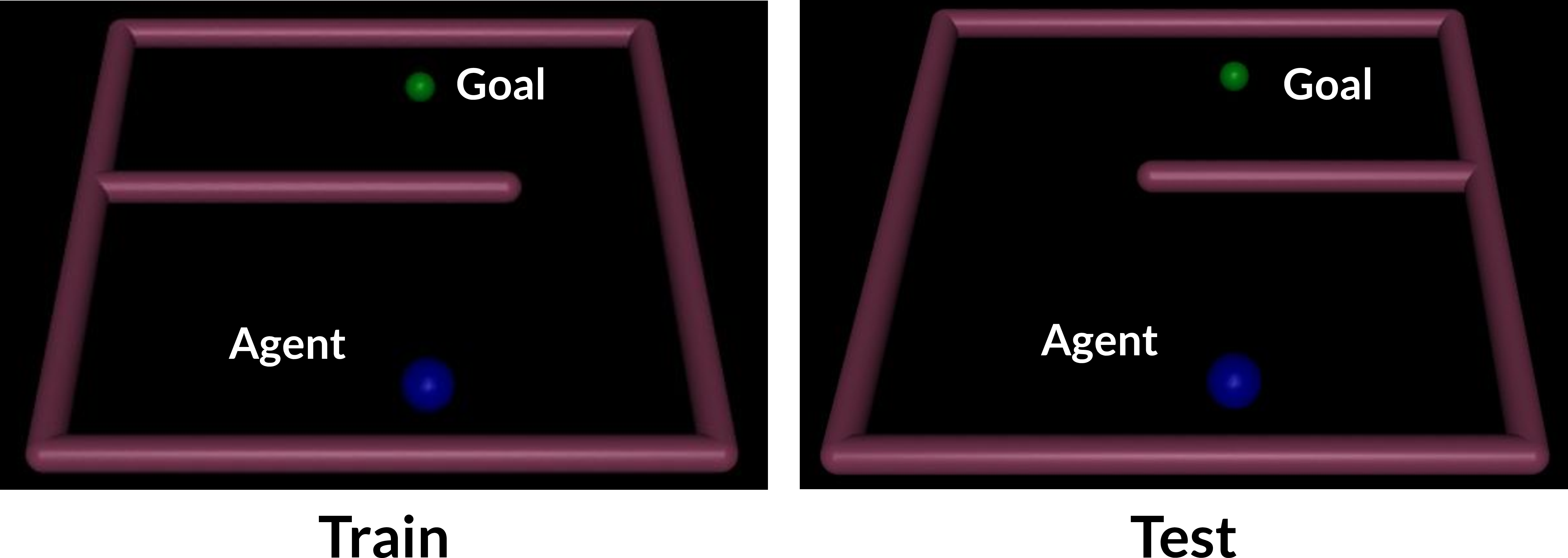
Figure 5:
The PointMaze environment: the agent must reach the goal by navigating around the wall that is on the left at train time and on the right at test time.
Even if distance is consistent across reasonable coverage distributions, the constant factor $K(\mathcal{D})$ could still be very large, making the bound weak or even vacuous. We therefore decided to test empirically whether EPIC distance predicts RL policy return, in a simple continuous control task PointMaze. The agent must navigate to a goal by moving around a wall that is on the left during training, and on the right during testing. The ground-truth reward function is the same in both variants, and so we might hope that learned reward functions will transfer. Note that optimal policies do not transfer: the optimal policy in the train environment will collide with the wall when deployed in the test environment, and vice-versa.

Figure 6:
EPIC distance predicts policy regret in the train and test tasks across three different reward learning methods.
We train reward functions using (a) regression to reward labels, (b) preference comparison between trajectories and (c) inverse reinforcement learning (IRL) on demonstrations. The training data is generated synthetically from a ground-truth reward. We find that regression and preference comparison learn a reward function with low EPIC distance to the ground-truth. Policies trained with these rewards achieve high return, and so low regret. By contrast, IRL has high EPIC distance to the ground-truth and high regret. This is in line with our theoretical result that EPIC distance predicts regret.
Conclusions
We believe that EPIC distance will be an informative addition to the evaluation toolbox for reward learning methods. EPIC is significantly faster than RL training, and is able to predict policy return even in unseen environments. We would therefore encourage researchers to report EPIC in addition to policy-based metrics when benchmarking reward learning algorithms.
It is important that our ability to accurately specify complex objectives keeps pace with the growth in reinforcement learning’s optimization power. Future AI systems such as virtual assistants or household robots will operate in complex open-ended environments involving extensive human interaction. Reaching human-level performance in these domains requires more than just human-level intelligence: we must also teach our AI systems the many nuances of human values. We expect techniques like EPIC to play a key role in building advanced and aligned AI, by letting us evaluate different models of human values trained via multiple techniques or data sources.
In particular, we believe EPIC can significantly improve the benchmarking of reward learning algorithms. By directly comparing the learned reward to a ground-truth reward, EPIC can provide a precise measurement of reward function quality, including its ability to transfer to new environments. By contrast, RL training cannot distinguish between learned rewards that capture user preferences, and those that merely happen to incentivize the right behaviour in the evaluation environment (but may fail in other environments). Moreover, RL training is slow and unreliable.

Figure 7:
Evaluation by RL training concludes the reward function was faulty after destroying the vase. EPIC can warn you the reward function differs from others before you train an agent.
Additionally, EPIC can help to validate a reward function prior to deployment. Using EPIC is particularly advantageous in settings where failures are unacceptable, since EPIC can compare reward functions offline on a pre-collected data set. By contrast, RL training requires taking actions in the environment to maximize the new reward. These actions could have irreversible consequences, such as a household robot knocking over a vase on the way to the kitchen if the learned reward incentivized speed but failed to penalize negative side-effects.
However, EPIC does have some drawbacks, and so is best used in conjunction with other methods. Most significantly, EPIC can only compare reward functions to one another, and cannot tell you what a particular reward function values. Given a set of unknown reward functions, at best EPIC can cluster them into similar and dissimilar groups. Other evaluation methods, such as interpretability or RL training, will be needed to understand what each cluster represents.
Additionally, EPIC can be overly conservative. EPIC is by design sensitive to differences in reward functions that might change the optimal policy, even if they lead to the same behaviour in the evaluation environment. This is desirable for safety critical applications, where robustness to distribution shift is critical, but this same property can lead to false alarms when the deployment environment is similar or identical to the evaluation environment. Currently the sensitivity of EPIC to off-distribution differences is controllable only at a coarse-grained level using the coverage distribution 𝒟. A promising direction for future work is to support finer-grained control based on distributions over or invariants on possible deployment environments.
Check out our ICLR paper for more information about EPIC. You can also find an implementation of EPIC on GitHub.
We would like to thank Jonathan Uesato, Neel Nanda, Vladimir Mikulik, Sebastian Farquhar, Cody Wild, Neel Alex and Victoria Krakovna for feedback on earlier drafts of this post.
