Recent years have demonstrated the potential of deep multi-agent reinforcement learning (MARL) to train groups of AI agents that can collaborate to solve complex tasks - for instance, AlphaStar achieved professional-level performance in the Starcraft II video game, and OpenAI Five defeated the world champion in Dota2. These successes, however, were powered by huge swaths of computational resources; tens of thousands of CPUs, hundreds of GPUs, and even TPUs were used to collect and train on a large volume of data. This has motivated the academic MARL community to develop MARL methods which train more efficiently.
DeepMind's AlphaStar attained professional level performance in StarCraft II, but required enormous amounts of
computational power to train.
Research in developing more efficient and effective MARL algorithms has focused on off-policy methods - which store and re-use data for multiple policy updates - rather than on-policy algorithms, which use newly collected training data before each update to the agents’ policies. This is largely due to the common belief that off-policy algorithms are much more sample-efficient than on-policy methods.
In this post, we outline our recent publication in which we re-examine many of these assumptions about on-policy algorithms. In particular, we analyze the performance of PPO, a popular single-agent on-policy RL algorithm, and demonstrate that with several simple modifications, PPO achieves strong performance in 3 popular MARL benchmarks while exhibiting a similar sample efficiency to popular off-policy algorithms in the majority of scenarios. We study the impact of these modifications through ablation studies and suggest concrete implementation and tuning practices which are critical for strong performance. We refer to PPO with these modifications as Multi-Agent PPO (MAPPO).
MAPPO
In this work, we focus our study on cooperative multi-agent tasks, in which a group of agents is trying to optimize a shared reward function. Each agent is decentralized and only has access to locally available information; for instance, in StarcraftII, an agent only observes agents/enemies within its vicinity. MAPPO, like PPO, trains two neural networks: a policy network (called an actor) $\pi_{\theta}$ to compute actions, and a value-function network (called a critic) $V_{\phi}$ which evaluates the quality of a state. MAPPO is a policy-gradient algorithm, and therefore updates $\pi_{\theta}$ using gradient ascent on the objective function.
We find find that several algorithmic and implementation details are particularly important for the practical performance of MAPPO, and outline them below:
1. Training Data Usage: It is typical for PPO to perform many epochs of updates on a batch of training data using mini-batch gradient descent. In single-agent settings, data is commonly reused through tens of training epochs and many mini-batches per epoch. We find that high data reuse is detrimental in multi-agent settings; we recommend using 15 training epochs for easy tasks, and 10 or 5 epochs for more difficult tasks. We hypothesize that the number of training epochs can control the challenge of non-stationarity in MARL. Non-stationarity arises from the fact that all agents’ policies are changing simultaneously throughout training; this makes it difficult for any given agent to properly update its policy since it does not know how the behavior of other agents will change. Using more training epochs will cause larger changes to the agents’ policies, which exacerbates the non-stationarity challenge. We additionally avoid splitting a batch of data into mini-batches, as this results in the best performance.
2. PPO Clipping: A core feature of PPO is the use of clipping in the policy and value function losses; this is used to constrain the policy and value functions from drastically changing between iterations in order to stabilize the training process (See this for a nice explanation of the PPO loss functions). The strength of the clipping is controlled by the $\epsilon$ hyperparameter: large $\epsilon$ allows for larger changes to the policy and value function. Similar to mini-batching, clipping may control the non-stationarity problem, as smaller $\epsilon$ values encourage agents’ policies to change less per gradient update. We generally observe that smaller $\epsilon$ values correspond to more stable training, whereas larger $\epsilon$ values result in more volatility in MAPPO’s performance.
3. Value normalization: the scale of the reward functions can vary vastly across environments, and having large reward scales can destabilize value learning. We thus use value normalization to normalize the regression targets into a range between 0 and 1 during value learning, and find that this often helps and never hurts MAPPO’s performance.
4. Value Function Input: Since the value-function is solely used during training updates and is not needed to compute actions, it can utilize global information to make more accurate predictions. This practice is common in other multi-agent policy gradient methods and is referred to as centralized training with decentralized execution. We evaluate MAPPO with several global state inputs, as well as local observation inputs.
We generally find that including both local and global information in the value function is most effective, and that omitting important local information can be highly detrimental. Furthermore, we observe that controlling the dimensionality of the value function input - for instance, by removing redundant or repeated features - further improves performance.
5. Death Masking: Unlike in single-agent settings, it is possible for certain agents to “die” or become inactive in the environment before the game terminates (this is true particularly in SMAC). We find that instead of using the global-state when an agent is dead, using a zero vector with the agent’s ID (which we call a death mask) as the input to the critic is more effective. We hypothesize that using a death mask allows the value function to more accurately represent states in which the agent is dead.
Results
We compare the performance of MAPPO and popular off-policy methods in three popular cooperative MARL benchmarks:
- StarcraftII (SMAC), in which decentralized agents must cooperate to defeat bots in various scenarios with a wide range of agent numbers (from 2 to 27).
- Multi-Agent Particle-World Environments (MPEs), in which small particle agents must navigate and communicate in a 2D box.
- Hanabi, a turn-based care game in which agents cooperatively take actions to stack cards in an ascending order in a manner similar to Solitaire.
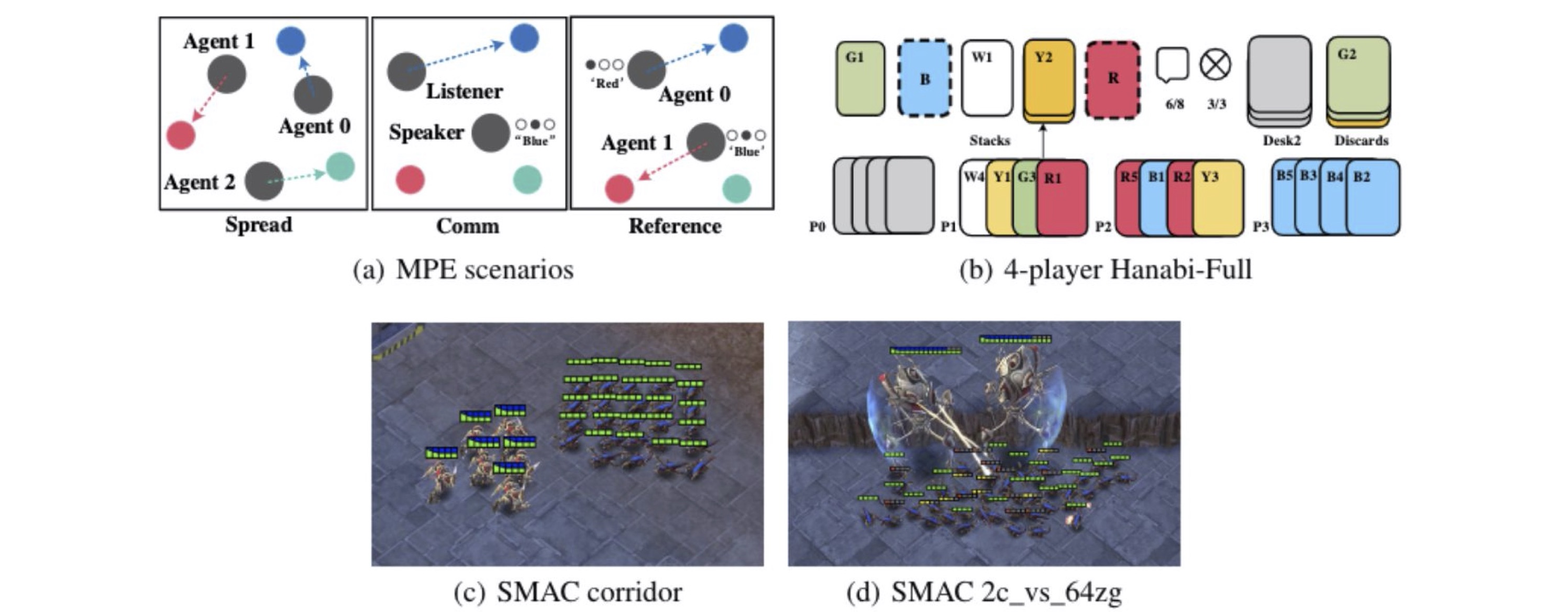
Task Visualizations.(a) The MPE domain. Spread (left): agents must cover all the landmarks and
do not have a color preference for the landmark they navigate to; Comm (middle): the listener needs to
navigate to a specific landmarks following the instruction from the speaker; Reference (right): both
agents only know the other's goal landmark and needs to communicate to ensure both agents move to the
desired target. (b) The Hanabi domain: 4-player Hanabi-Full . (c) The corridor map in the SMAC domain.
(d) The 2c vs. 64zg map in the SMAC domain.
Overall, we observe that in the majority of environments, MAPPO achieves results comparable or superior to off-policy methods with comparable sample-efficiency.
SMAC Results
In SMAC, we compare MAPPO and IPPO to value-decomposition off-policy methods including QMix, RODE, and QPLEX.
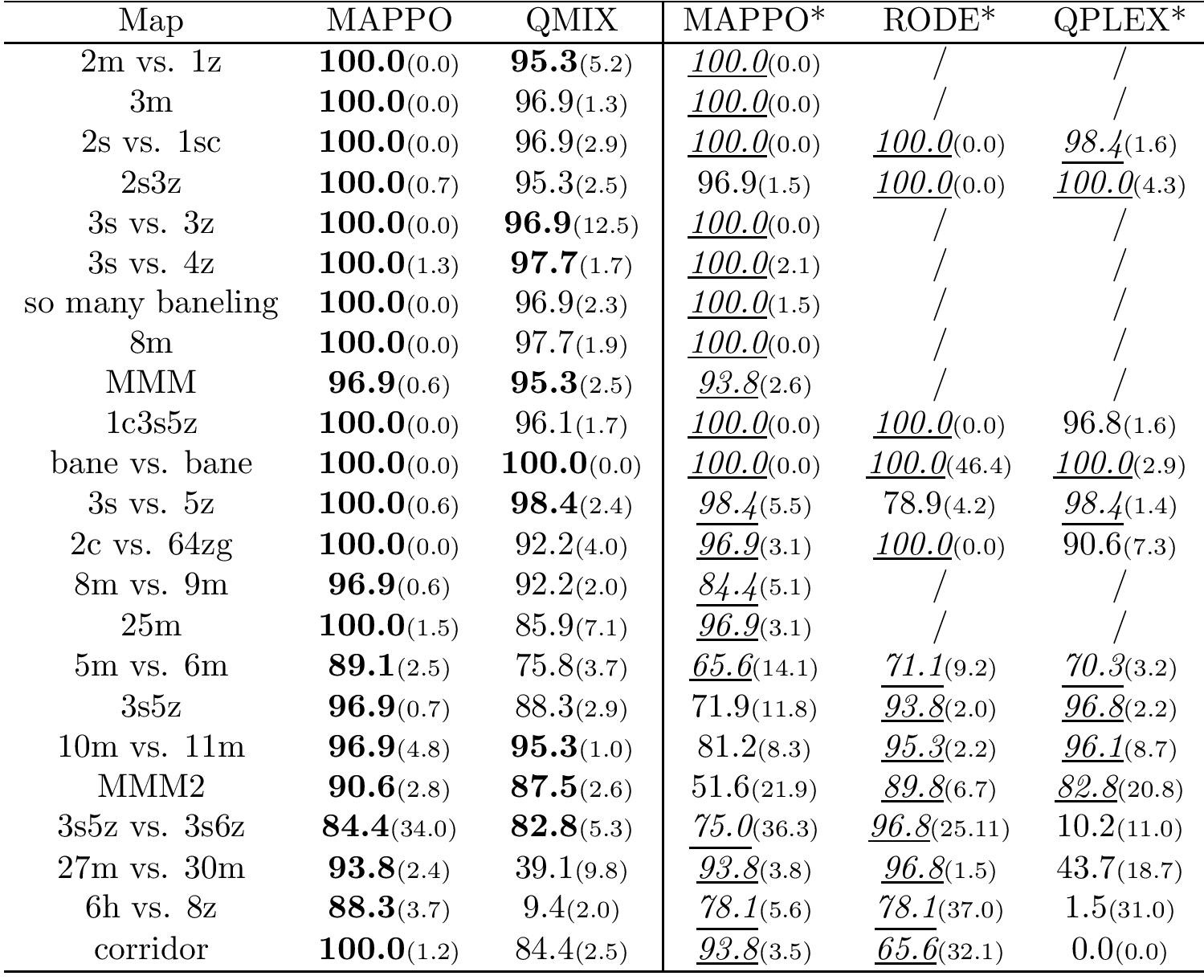
Median evaluation win rate and standard deviation on all the SMAC maps for different methods,
Columns with "*'' display results using the same number of timesteps as RODE. We bold all values
within 1 standard deviation of the maximum and among the "*'' columns, we denote all values within
1 standard deviation of the maximum with underlined italics.
We again observe that MAPPO generally outperforms QMix and is comparable with RODE and QPLEX.
MPE Results
We evaluate MAPPO with centralized value functions and PPO with decentralized value functions (IPPO) and compare it to several off-policy methods, including MADDPG and QMix.
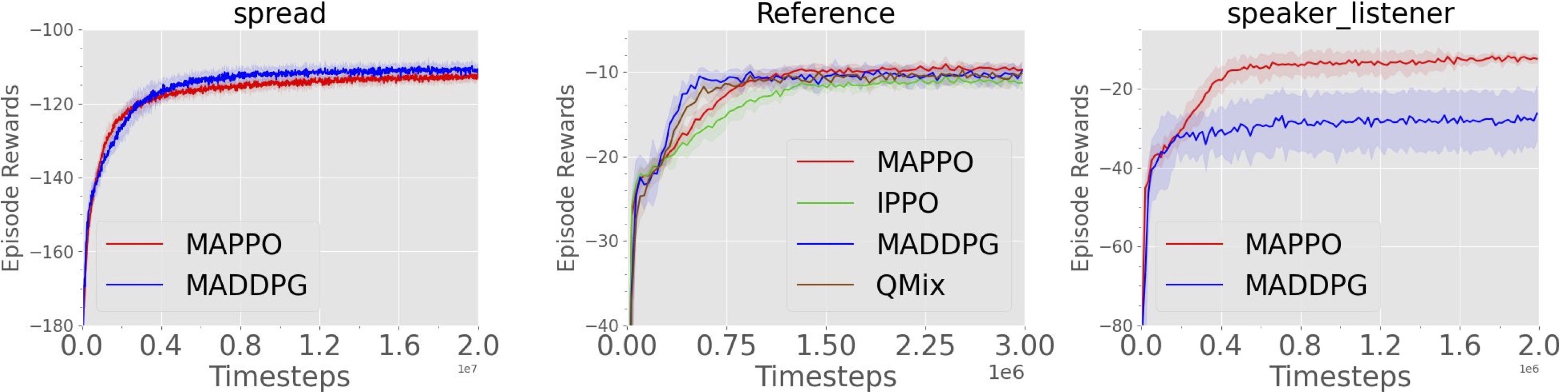
Training curves demonstrating the performance of various algorithms on the MPEs.
Hanabi Results
We evaluate MAPPO in the 2-player full-scale Hanabi game and compare it with several strong off-policy methods, including SAD, a Q-learning variant which has been successful in the Hanabi game, and a modified version of Value Decomposition Networks (VDN).
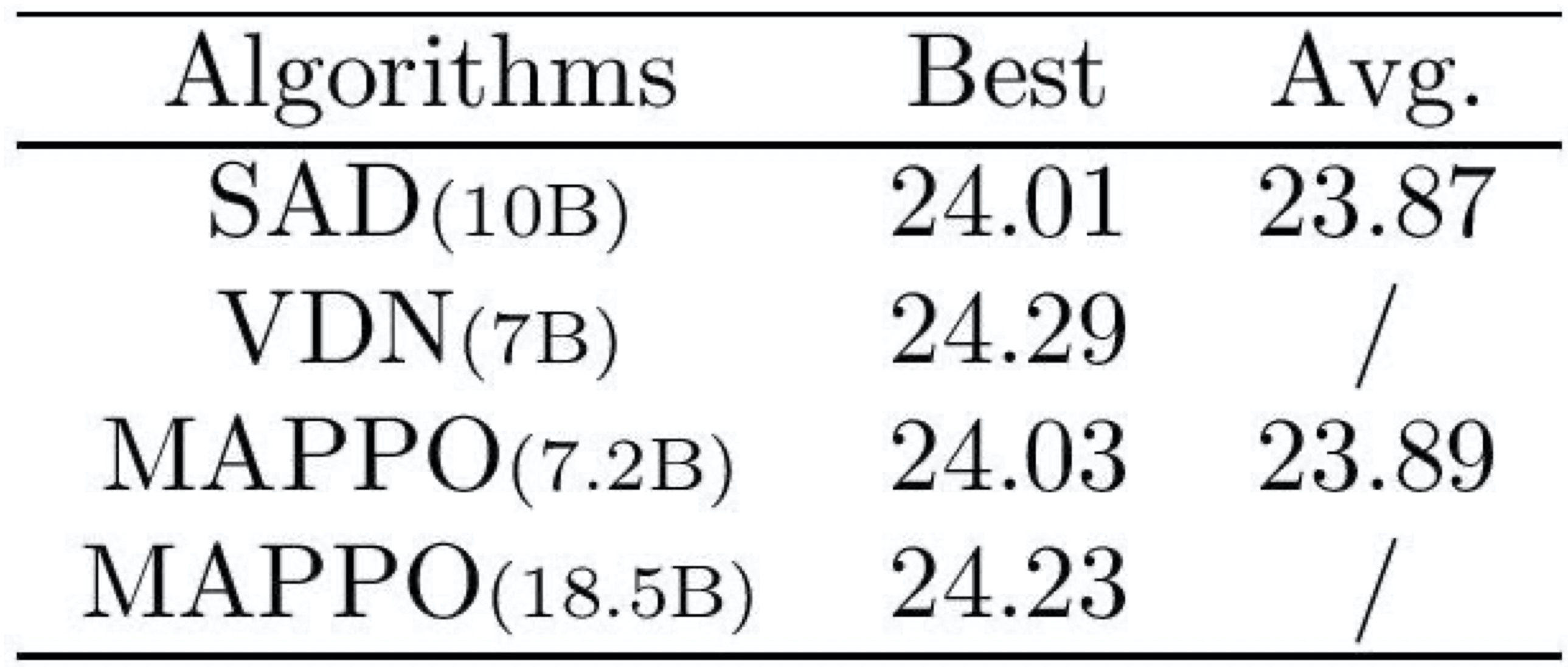
Best and average evaluation scores of various algorithms in 2 player Hanabi-Full. Values in parentheses indicate the number of timesteps used.
We see that MAPPO achieves comparable performance with SAD despite using 2.8B fewer environment steps, and continues to improve with more environment steps. VDN surpasses MAPPO’s performance; VDN, however, uses additional training tasks which aid the training process. Incorporating these tasks into MAPPO would be an interesting direction of future investigation.
Conclusions
In this work, we aimed to demonstrate that with several modifications, PPO-based algorithms can achieve strong performance in multi-agent settings and serve as a good benchmark for MARL. Additionally, this suggests that despite a heavy emphasis on developing new off-policy methods for MARL, on-policy methods such as PPO can be a promising direction for future research.
Our empirical investigations demonstrating the effectiveness of MAPPO, as well as our studies of the impact of five key algorithmic and implementation techniques on MAPPO’s performance, can lead to several future avenues of research. These include:
- Investigating MAPPO’s performance on a wider range of domains, such as competitive games or multi-agent settings with continuous action spaces. This would further evaluate MAPPO’s versatility.
- Developing domain-specific variants of MAPPO to further improve performance in specific settings.
- Developing a greater theoretical understanding as to why MAPPO can perform well in multi-agent settings.
This post is based on the paper “The Surprising Effectiveness of PPO in Cooperative Multi-Agent Games”. You can find our paper here, and we provide code to to reproduce our experiments.
