The case fatality rate quantifies how dangerous COVID-19 is, and how risk of death varies with strata like geography, age, and race. Current estimates of the COVID-19 case fatality rate (CFR) are biased for dozens of reasons, from under-testing of asymptomatic cases to government misreporting. We provide a careful and comprehensive overview of these biases and show how statistical thinking and modeling can combat such problems. Most importantly, data quality is key to unbiased CFR estimation. We show that a relatively small dataset collected via careful contact tracing would enable simple and potentially more accurate CFR estimation.

What is the case fatality rate, and why do we need to estimate it?

The case fatality rate (CFR) is the proportion of fatal COVID-19 cases. The term is ambiguous, since its value depends on the definition of a ‘case.’ No perfect definition of the case fatality rate exists, but in this article, I define it loosely as the proportion of deaths among all COVID-19-infected individuals.

The CFR is a measure of disease severity. Furthermore, the relative CFR (the ratio of CFRs between two subpopulations) enables data-driven resource-allocation by quantifying relative risk. In other words, the CFR tells us how drastic our response needs to be; the relative CFR helps us allocate scarce resources to populations that have a higher risk of death.

Although the CFR is defined as the number of fatal infections, we can not expect that dividing the number of deaths by the number of cases will give us a good estimate of the CFR. The problem is that both the numerator (#deaths) and the denominator (#infections) of this fraction are uncertain for systematic reasons due to the way data is collected. For this reason, we call that estimator “the naive estimator”, or simply deaths/cases, and denote it as $E_{\rm naive}$.

Why are (all) CFR estimates biased?

In short, all CFR estimates are biased because the publicly available data is biased. We have reasson to believe that we are losing at least 99.8% of our sample efficiency due to this bias. There is a “butterfly effect” caused by non-random sampling: a tiny correlation between the sampling method and the quantity of interest can have huge, destructive effects on an estimator. Even assuming a tiny 0.005 correlation between the population we test and the population infected, testing 10,000 people for SARS-CoV-2 is equivalent to testing 20 individuals randomly. For estimating the fatality rate, the situation is even worse, since we have ample evidence that severe cases are preferentially diagnosed and reported. In the words of Xiao-Li Meng, “compensating for [data] quality with quantity is a doomed game.” In our HDSR article, we show that in order for the naive estimator $E_{\rm naive}$ to converge to the correct CFR, there must be no correlation between fatality and being tested — but severe cases are much more likely to be tested. Government and health organizations have been explicitly reserving tests for severe cases due to shortages, and severe cases are likely to go to the hospital and get tested, while asymptomatic ones are not.

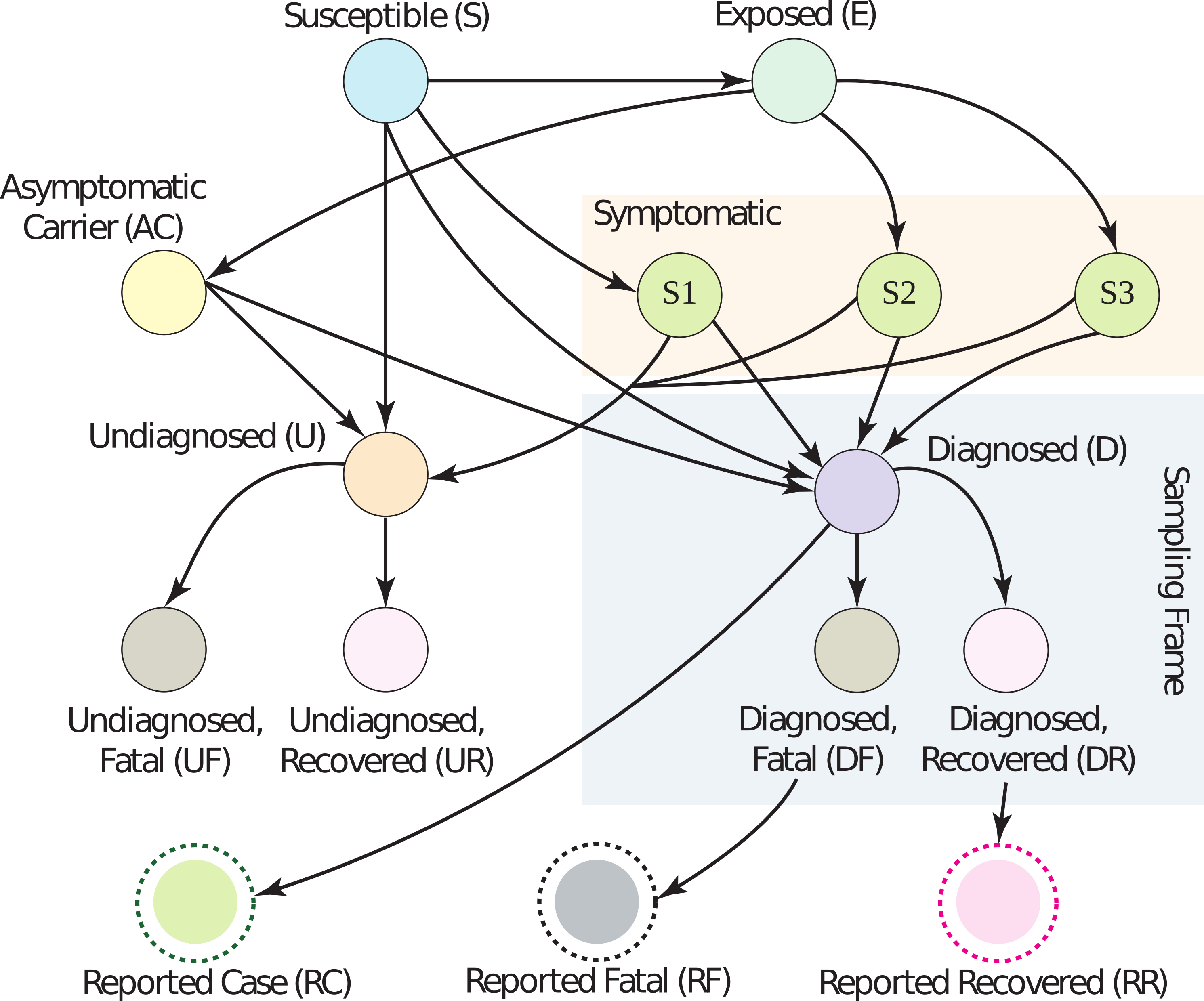
The primary source of COVID-19 data is population surveillance: county-level aggregate statistics reported by medical providers who diagnose patients on-site. Usually, somebody feels sick and goes to a hospital, where they get tested and diagnosed. The hospital reports the number of cases, deaths, and sometimes recoveries to local authorities, who release the data on a weekly basis. In reality, there are many differences in data collection between nations, local governments, and even hospitals.

Dozens of biases are induced by this method of surveillance, falling coarsely into five categories: under-ascertainment of mild cases, time lags, interventions, group characteristics (e.g. age, sex, race), and imperfect reporting and attribution. An extensive (but not exhaustive) discussion of the magnitude and direction of these biases is in Section 2 of our article. Without mincing words, current data is extremely low quality. The vast majority of people who get COVID-19 go undiagnosed, there are misattributions of symptoms and deaths, data reported by governments is often (and perhaps purposefully) incorrect, cases are defined inconsistently across countries, and there are many time-lags. (For example, cases are counted as ‘diagnosed’ before they are ‘fatal’, leading to a downward bias in the CFR if the number of cases is growing over time.) Figure 1 has a graphical model describing these many relationships; look to the paper for a detailed explanation of what biases occur across each edge.

Correcting for biases is sometimes possible using outside data sources, but can result in a worse estimator overall due to partial bias cancellation. This is easier to see through example than it is to explain. Assume the true CFR is some value $p$ in the range 0 to 1 (i.e., deaths/infections is equal to $p$). Then, assume that because of under-ascertainment of mild cases, there are too many fatal cases being reported, which means $E_{\rm naive}$ converges to $bp > p$ (in other words, it is higher than it should be by a factor of $b$). Also assume the time-lag between diagnosis and death causes the proportion of deaths to diagnoses to decrease by the same factor $b$. Then, $E_{\rm naive}$ converges to $b(p/b)=p$, the correct value. So, even though it might seem to be an objectively good idea to correct for time-lag between diagnosis and death, it would actually result in a worse estimator in this case, since time-lag is helping us out by cancelling out under-ascertainment.

The mathematical form of the naive estimator $E_{\rm naive}$ allows us to see easily what we need to do to make it unbiased. With $p$ being the true CFR, $q$ being the reporting rate, and $r$ being the covariance between death and diagnosis, the mean of $E_{\rm naive}$ is:

This equation is pretty easy to understand. We wanted $\mu$ to be equal to $p$. Instead, we got an expression that depends on $r$, $q$, and $N$. The $r/q$ term is the price we pay if people who are diagnosed are more likely to eventually die. We want $r/q=0$, but in practice, $r/q$ is probably much larger than $p$. (Actually, if we assume the CFR is around 0.5% and the measured CFR is 5.2% on June 22, 2020, then $r/q \ge 0.047 \gg 0.005$.) In other words, $r/q$ is the bias, and it can be large. The term $p$ is the true CFR, which we want. And the factor $(1−(1−q)^N)$ is what we pay because of non-response; however, it’s not a big deal, because it disappears quite fast as the number of samples $N$ grows. So really, our primary concern should be achieving $r=0$, because — and I cannot stress this enough — $r/q$ does not decrease with more samples; it only decreases with higher quality samples.

What are strategies for fixing the bias?

In our article, we outline a testing procedure that helps fix some of the above dataset biases. If we collect data properly, even the naive estimator $E_{\rm naive}$ has good performance.

In particular, data should be collected via a procedure like the following:

1. Diagnose person $P$ with COVID-19 by any means, like at a hospital.

2. Reach out to contacts of $P$. If a contact has no symptoms, ask them to commit to getting a COVID-19 test.

3. Test committed contacts after the virus has incubated.

4. Keep data with maximum granularity while respecting ethics/law.

5. Follow up after a few weeks to ascertain the severity of symptoms.

6. For committed contacts who didn’t get tested, call and note if they are asymptomatic.

This protocol is meant to decrease the covariance between fatality and diagnosis. If patients commit to testing before they develop symptoms, this covariance simply cannot exist. However, there may still be issues with people dropping out of the study; if this is a problem in practice, it can be mitigated by a combination of incentives (payments) and consistent follow-ups.

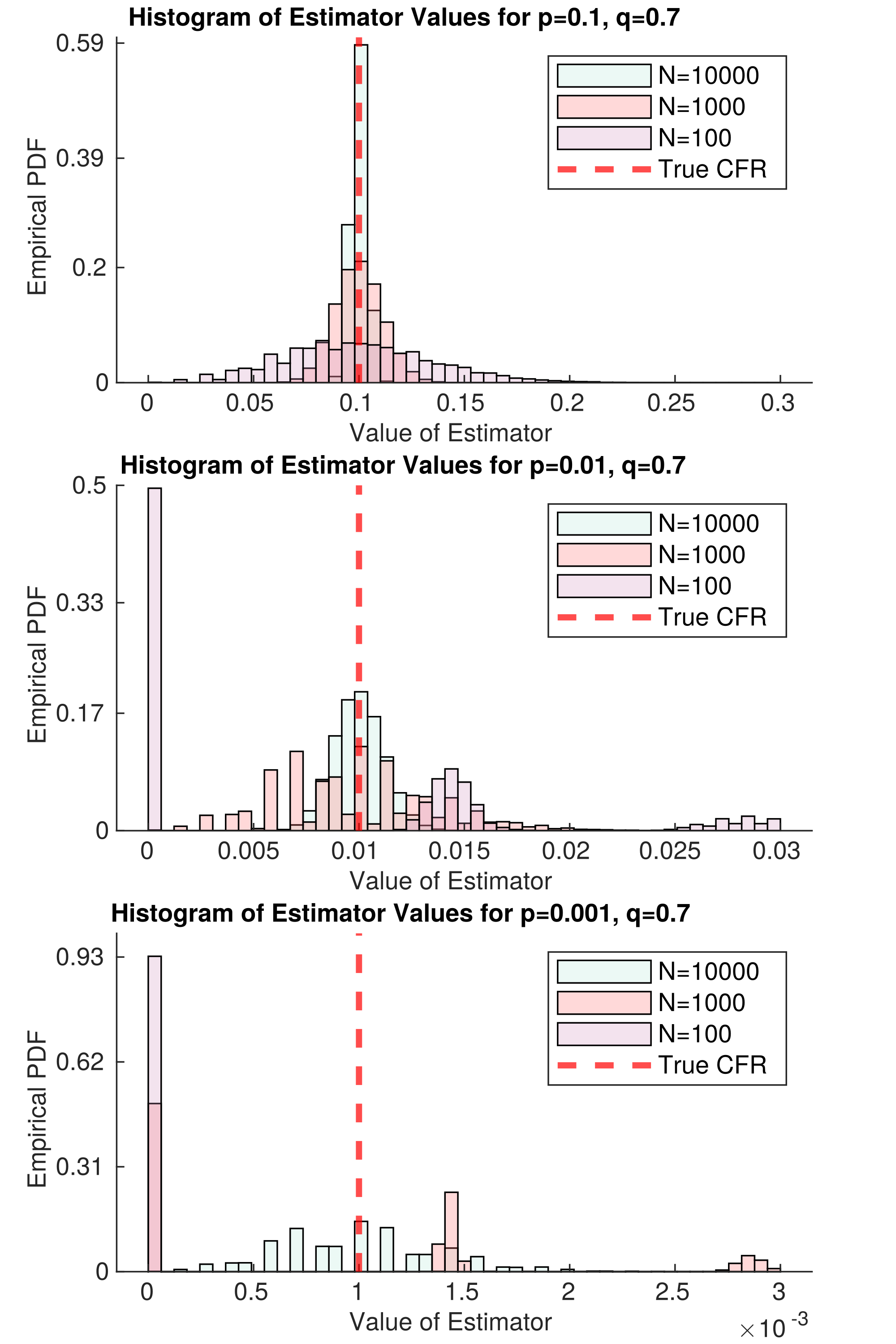
Figure 2 represents an idealized version of this study. In the best case scenario, there is no covariance between death and diagnosis. Then, we only need $N=66$ samples for our estimator of the CFR to be approximately unbiased, even if $p=0.001$ ($1/1000$ cases die). Problems remain in the case that $p$ is small; namely, death is so rare that we need tons of samples to decrease the variance of our estimator. This will require lots of samples. But even if no deaths are observed, we get a lot of information about $p$; for example, if $N=1000$ and we have not observed a single death, then we can confidently say that $p<0.01$ within the population we are sampling. This is simply because in the second panel of Figure 2, there is nearly zero mass in the $N=1000$ histogram at $E_{\rm naive} = 0$. With this in mind, we could find the largest possible p that is consistent with our data — this would be a conservative upper bound on $p$, but it would be much closer to the true value than we can get with current data.

This strategy mostly resolves what we believe is the largest set of biases in CFR estimation — under-ascertainment of mild cases and time-lags. However, there will still be lots of room for improvement, like understanding the dependency of CFR on age, sex, and race. (In other words, the CFR is a random quantity itself, depending on the population being sampled.) Distinctions between CFRs of these strata may be quite small, requiring a lot of high-quality data to analyze. If $p$ is extremely low, like 0.001, this may require collecting $N=100,000$ or $N=1,000,000$ samples per group. Perhaps there are ways to lower that number by pooling samples. Even though making correct inferences will require careful thought (as always), this data collection strategy will make it much simpler.

I’d like to re-emphasize a point here: collecting data as above will make the naive estimator $E_{\rm naive}$ unbiased for the sampled population. But the sampled population may not be the population we care about. However, there is a set of statistical techniques collectively called ‘post-stratification’ that can help deal with this problem effectively — see Mr. P.

If you read our academic article, we provide some thoughts on how to use time-series data and outside information to correct time-lags and relative reporting rates. Our work was very heavily based on one of Nick Reich’s papers. However, as I claimed earlier, even fancy estimators cannot overcome fundamental problems with data collection. I’ll defer discussion of that estimator, and the results we got from it, to the article. I’d love to hear your thoughts on it.

CFR estimation is clearly a difficult problem — but with proper data collection and estimation guided by data scientists, I still believe that we can get a useful CFR estimate. This will help guide public policy decisions about this urgent and ongoing pandemic.

This blog post is based on the following paper:

• On Identifying and Mitigating Bias in the Estimation of the COVID-19 Case Fatality Rate.
  Anastasios Angelopoulos, Reese Pathak, Rohit Varma, Michael I. Jordan
  Harvard Data Science Review Special Issue 1 — COVID-19: Unprecedented Challenges and Chances. 2020.