This post is cross-listed on the CMU ML blog.

The history of machine learning has largely been a story of increasing abstraction. In the dawn of ML, researchers spent considerable effort engineering features. As deep learning gained popularity, researchers then shifted towards tuning the update rules and learning rates for their optimizers. Recent research in meta-learning has climbed one level of abstraction higher: many researchers now spend their days manually constructing task distributions, from which they can automatically learn good optimizers. What might be the next rung on this ladder? In this post we introduce theory and algorithms for unsupervised meta-learning, where machine learning algorithms themselves propose their own task distributions. Unsupervised meta-learning further reduces the amount of human supervision required to solve tasks, potentially inserting a new rung on this ladder of abstraction.

We start by discussing how machine learning algorithms use human supervision to find patterns and extract knowledge from observed data. The most common machine learning setting is regression, where a human provides labels $Y$ for a set of examples $X$. The aim is to return a predictor that correctly assigns labels to novel examples. Another common machine learning problem setting is reinforcement learning (RL), where an agent takes actions in an environment. In RL, humans indicate the desired behavior through a reward function that the agent seeks to maximize. To draw a crude analogy to regression, the environment dynamics are the examples $X$, and the reward function gives the labels $Y$. Algorithms for regression and RL employ many tools, including tabular methods (e.g., value iteration), linear methods (e.g., linear regression) kernel-methods (e.g., RBF-SVMs), and deep neural networks. Broadly, we call these algorithms learning procedures: processes that take as input a dataset (examples with labels, or transitions with rewards) and output a function that performs well (achieves high accuracy or large reward) on the dataset.

Machine learning research is similar to the control room for large physics experiments. Researchers have a number of knobs they can tune which affect the performance of the learning procedure. The right setting for the knobs depends on the particular experiment: some settings work well for high-energy experiments; others work well for ultracold atom experiments. Figure Credit.

Similar to lab procedures used in physics and biology, the learning procedures used in machine learning have many knobs¹ that can be tuned. For example, the learning procedure for training a neural network might be defined by an optimizer (e.g., Nesterov, Adam) and a learning rate (e.g., 1e-5). Compared with regression, learning procedures specific to RL (e.g., DDPG) often have many more knobs, including the frequency of data collection and how frequently the policy is updated. Finding the right setting for the knobs can have a large effect on how quickly the learning procedure solves a task, and a good configuration of knobs for one learning procedure may be a bad configuration for another.

Meta-Learning Optimizes Knobs of the Learning Procedure

While machine learning practitioners often carefully tune these knobs by hand, if we are going to solve many tasks, it may be useful to automatic this process. The process of setting the knobs of learning procedures via optimization is called meta-learning [Thrun 1998]. Algorithms that perform this optimization problem automatically are known as meta-learning algorithms. Explicitly tuning the knobs of learning procedures is an active area of research, with various researchers looking at tuning the update rules [Andrychowicz 2016, Duan 2016, Wang 2016], weight initialization [Finn 2017], network weights [Ha 2016], network architectures [Gaier 2019], and other facets of learning procedures.

To evaluate a setting of knobs, meta-learning algorithms consider not one task but a distribution over many tasks. For example, a distribution over supervised learning tasks may include learning a dog detector, learning a cat detector, and learning a bird detector. In reinforcement learning, a task distribution could be defined as driving a car in a smooth, safe, and efficient manner, where tasks differ by the weights they place on smoothness, safety, and efficiency. Ideally, the task distribution is designed to mirror the distribution over tasks that we are likely to encounter in the real world. Since the tasks in a task distribution are typically related, information from one task may be useful in solving other tasks more efficiently. As you might expect, a knob setting that works best on one distribution of tasks may not be the best for another task distribution; the optimal knob setting depends on the task distribution.

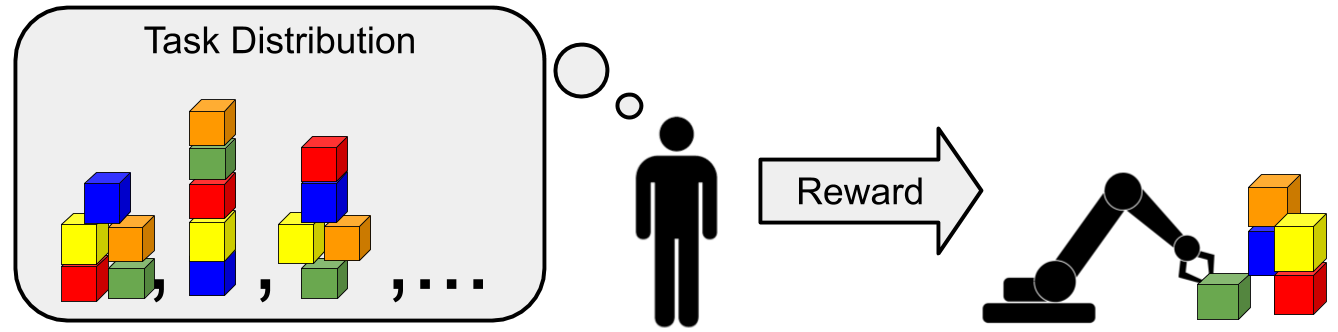
An illustration of meta-learning, where tasks correspond to arranging blocks into different types of towers. The human has a particular block tower in mind and rewards the robot when it builds the correct tower. The robot's aim is to build the correct tower as quickly as possible.

In many settings we want to do well on a task distribution to which we have only limited access. For example, in a self-driving car, tasks may correspond to finding the optimal balance of smoothness, safety, and efficiency for each rider, but querying riders to get rewards is expensive. A researcher can attempt to manually construct a task distribution that mimics the true task distribution, but this can be quite challenging and time consuming. Can we avoid having to manually design such task distributions?

To answer this question, we must understand where the benefits of meta-learning come from. When we define task distributions for meta-learning, we do so with some prior knowledge in mind. Without this prior information, tuning the knobs of a learning procedure is often a zero-sum game: setting the knobs to any configuration will accelerate learning on some tasks while slowing learning on other tasks. Does this suggest there is no way to see the benefit of meta-learning without the manual construction of task distributions? Perhaps not! The next section presents an alternative.

Optimizing the Learning Procedure with Self-Proposed Tasks

If designing task distributions is the bottleneck in applying meta-learning algorithms, why not have meta-learning algorithms propose their own tasks? At first glance this seems like a terrible idea, because the No Free Lunch Theorem suggests that this is impossible, without additional knowledge. However, many real-world settings do provide a bit of additional information, albeit disguised as unlabeled data. For example, in regression, we might have access to an unlabeled dataset and know that the downstream tasks will be labeled versions of this same image dataset. In a RL setting, a robot can interact with its environment without receiving any reward, knowing that downstream tasks will be constructed by defining reward functions for this very environment (i.e. the real world). Seen from this perspective, the recipe for unsupervised meta-learning (doing meta-learning without manually constructed tasks) becomes clear: given unlabeled data, construct task distributions from this unlabeled data or environment, and then meta-learn to quickly solve these self-proposed tasks.

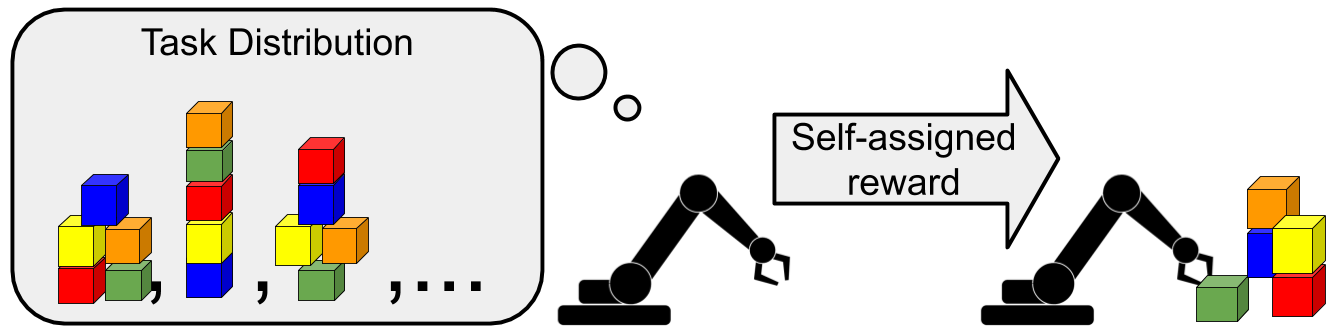
In unsupervised meta-learning, the agent proposes its own tasks, rather than relying on tasks proposed by a human.

How can we use this unlabeled data to construct task distributions which will facilitate learning downstream tasks? In the case of regression, prior work on unsupervised meta-learning [Hsu 2018, Khodadadeh 2019] clusters an unlabeled dataset of images and then randomly chooses subsets of the clusters to define a distribution of classification tasks. Other work [Jabri 2019] look at an RL setting: after exploring an environment without a reward function to collect a set of behaviors that are feasible in this environment, these behaviors are clustered and used to define a distribution of reward functions. In both cases, even though the tasks constructed can be random, the resulting task distribution is not random, because all tasks share the underlying unlabeled data — the image dataset for regression and the environment dynamics for reinforcement learning. The underlying unlabeled data are the inductive bias with which we pay for our free lunch.

Let us take a deeper look into the RL case. Without knowing the downstream tasks or reward functions, what is the “best” task distribution for “practicing” to solve tasks quickly? Can we measure how effective a task distribution is for solving unknown, downstream tasks? Is there any sense in which one unsupervised task proposal mechanism is better than another? Understanding the answers to these questions may guide the principled development of meta-learning algorithms with little dependence on human supervision. Our work [Gupta 2018], takes a first step towards answering these questions. In particular, we examine the worst-case performance of learning procedures, and derive an optimal unsupervised meta-reinforcement learning procedure.

Optimal Unsupervised Meta-Learning

To answer the questions posed above, our first step is to define an optimal meta-learner for the case where the distribution of tasks is known. We define an optimal meta-learner as the learning procedure that achieves the largest expected reward, averaged across the distribution of tasks. More precisely, we will compare the expected reward for a learning procedure $f$ to that of best learning procedure $f^*$, defining the regret of $f$ on a task distribution $p$ as follows:

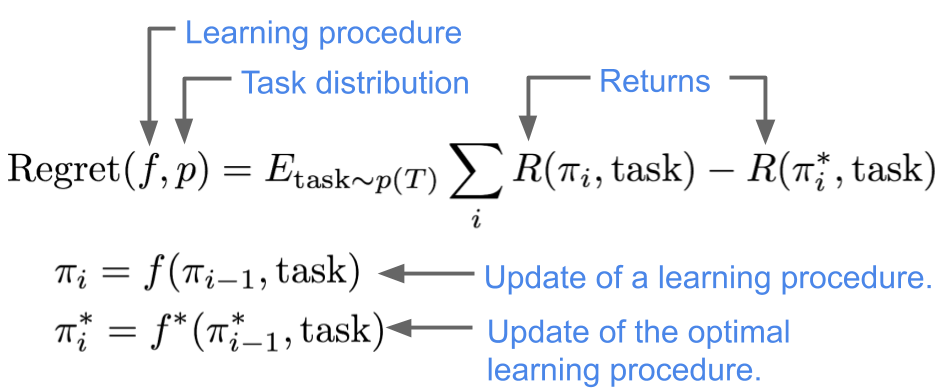
Extending this definition to the case of unsupervised meta-learning, an optimal unsupervised meta-learner can be defined as a meta-learner that achieves the minimum worst-case regret across all possible task distributions that may be encountered in the environment. In the absence of any knowledge about the actual downstream task, we resort to a worst case formulation. An unsupervised meta-learning algorithm will find a single learning procedure $f$ that has the lowest regret against an adversarially chosen task distribution $p$:

Our work analyzes how exactly we might obtain such an optimal unsupervised meta-learner, and provides bounds on the regret that it might incur in the worst case. Specifically, under some restrictions on the family of tasks that might be encountered at test-time, the optimal distribution for an unsupervised meta-learner to propose is uniform over all possible tasks.

The intuition for this is straightforward: if the test time task distribution can be chosen adversarially, the algorithm must make sure it is uniformly good over all possible tasks that might be encountered. As a didactic example, if test-time reward functions were restricted to the class of goal-reaching tasks, the regret for reaching a goal at test-time is inverse related to the probability of sampling that goal during training-time. If any one of the goals $g$ has lower density than the others, an adversary can propose a task distribution solely consisting of reaching that goal $g$ causing the learning procedure to incur a higher regret. This example suggests that we can find an optimal unsupervised meta-learner using a uniform distribution over goals. Our paper formalizes this idea and extends it to broader classes task distributions.

Now, actually sampling from a uniform distribution over all possible tasks is quite challenging. Several recent papers have proposed RL exploration methods based on maximizing mutual information [Achiam 2018, Eysenbach 2018, Gregor 2016, Lee 2019, Sharma 2019]. In this work, we show that these methods provide a tractable approximation to the uniform distribution over task distributions. To understand why this is, we can look at the form of a mutual information considered by [Eysenbach 2018], between states $s$ and latent variables $z$:

In this objective, the first marginal entropy term is maximized when there is a uniform distribution over all possible tasks. The second conditional entropy term ensures consistency, by making sure that for each $z$, the resulting distribution of $s$ is narrow. This suggests constructing unsupervised task-distributions in an environment by optimizing mutual information gives us a provably optimal task distribution, according to our notion of min-max optimality.

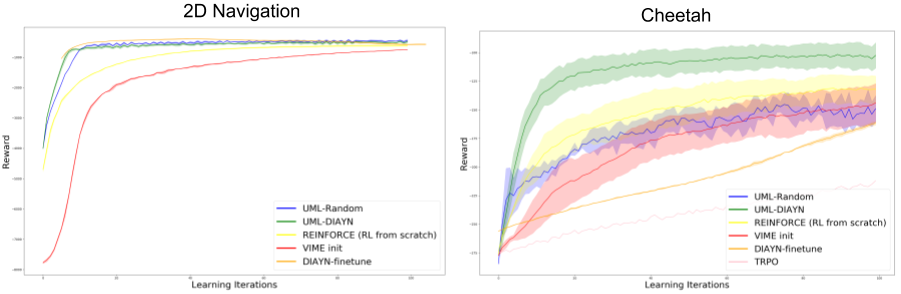
While the analysis makes some limiting assumptions about the forms of tasks encountered, we show how this analysis can be extended to provide a bound on the performance in the most general case of reinforcement learning. It also provides empirical gains on several simulated environments as compared to methods which train from scratch, as shown in the Figure below.

Summary & Discussion

In summary:

• Learning procedures are recipes for converting datasets into function approximators. Learning procedures have many knobs, which can be tuned by optimizing the learning procedures to solve a distribution of tasks.

• Manually designing these task distributions is challenging, so a recent line of work suggests that the learning procedure can use unlabeled data to propose its own tasks for optimizing its knobs.

• These unsupervised meta-learning algorithms allow for learning in regimes previously impractical, and further expand that capability of machine learning methods.

• This work closely relates to other works on unsupervised skill discovery, exploration and representation learning, but explicitly optimizes for transferability of the representations and skills to downstream tasks.

A number of open questions remain about unsupervised meta-learning:

• Unsupervised learning is closely connected to unsupervised meta-learning: the former uses unlabeled data to learn features, while the second uses unlabeled data to tune the learning procedure. Might there be some unifying treatment of both approaches?

• Our analysis only proves that task proposal based on mutual information is optimal for memoryless meta-learning algorithms. Meta-learning algorithms with memory, which we expect will perform better, may perform best with different task proposal mechanisms.

• Scaling unsupervised meta learning to leverage large-scale datasets and complex tasks holds the promise of acquiring learning procedures for solving real-world problems more efficiently than our current learning procedures.

Check out our paper for more experiments and proofs: https://arxiv.org/abs/1806.04640

Acknowledgments

Thanks to Jake Tyo, Conor Igoe, Sergey Levine, Chelsea Finn, Misha Khodak, Daniel Seita, and Stefani Karp for their feedback.