To operate successfully in a complex and changing environment, learning agents must be able to acquire new skills quickly. Humans display remarkable skill in this area — we can learn to recognize a new object from one example, adapt to driving a different car in a matter of minutes, and add a new slang word to our vocabulary after hearing it once. Meta-learning is a promising approach for enabling such capabilities in machines. In this paradigm, the agent adapts to a new task from limited data by leveraging a wealth of experience collected in performing related tasks. For agents that must take actions and collect their own experience, meta-reinforcement learning (meta-RL) holds the promise of enabling fast adaptation to new scenarios. Unfortunately, while the trained policy can adapt quickly to new tasks, the meta-training process requires large amounts of data from a range of training tasks, exacerbating the sample inefficiency that plagues RL algorithms. As a result, existing meta-RL algorithms are largely feasible only in simulated environments. In this post, we’ll briefly survey the current landscape of meta-RL and then introduce a new algorithm called PEARL that drastically improves sample efficiency by orders of magnitude. (Check out the research paper and the code.)

A look back: what’s happened in meta-RL?

Two years ago this blog featured a post called Learning to Learn. In addition to presenting a new algorithm, this post surveyed the surge of interest in meta-learning that had recently taken place. The key idea then and now was to reduce the problem to one we already know how to solve. Traditionally in machine learning, we are given a set of data points that we can use to fit a model. In meta-learning, we replace this dataset with a set of datasets, each of which corresponds to a learning problem. As long as the procedure for learning these problems (what we call adaptation) is differentiable, we can optimize it in an outer loop (meta-training) with gradient descent, as usual. Once trained, the adaptation procedure can quickly solve a new related task from a small amount of data.

Recent meta-RL advancements. From left to right: meta-learned one-shot imitation from observing humans (Yu et al. 2018), adapting to a broken leg with meta-model-based RL (Nagabandi et al. 2019), extrapolating beyond the training task distribution with evolved policy gradients (Hoothooft et al. 2018)

At the time, most other meta-learning work focused on few-shot image classification. In the years since, meta-learning has been applied to a broader range of problems such as visual navigation, machine translation, and speech recognition, to name a few. Reinforcement learning (RL) is a challenging but exciting target for meta-learning methods, as it holds the promise of enabling agents to quickly learn new tasks — a vital skill for robots deployed in a complex and changing world. Meta-learning is especially appealing to deep RL since sample complexity is a particularly pertinent problem. Two years ago, a few meta-learning papers (RL2, Wang et al., and MAML) presented initial results in applying meta-learning to RL in the limited setting of policy gradients and dense rewards. Since then, there has been a flurry of interest, with papers applying meta-learning ideas to a broader range of settings such as learning from human demonstrations, imitation learning, and model-based RL. In addition to meta-learning model parameters, we’ve also learned hyperparameters and loss functions. To tackle sparse reward settings, we’ve seen a method for meta-learning exploration strategies.

Despite these advances, sample efficiency remains a challenge. As we look towards applying meta-RL to more complex tasks on real-world systems, rapid adaptation for complex tasks will require efficient exploration strategies, and good meta-training sample efficiency will be necessary for learning in the real world. We will now examine each of these problems in turn as we develop an algorithm that aims to address both.

The lustre of off-policy meta-RL

While policy gradient RL algorithms can achieve high performance on complex high-dimensional control tasks (e.g., controlling a simulated humanoid robot to run), they are woefully sample inefficient. For example, the state-of-the-art policy gradient method PPO requires 100 million samples to learn a good policy for humanoid. If we were to run this algorithm on a real robot, running continuously with a 20 Hz controller and without counting time for resets, it would take nearly two months to learn this policy. This sample inefficiency is largely because the data to form the policy gradient update must be sampled from the current policy, precluding the re-use of previously collected data during training. Recent off-policy algorithms (TD3, SAC) have matched the performance of policy gradient algorithms while requiring up to 100X fewer samples. If we could leverage these algorithms for meta-RL, weeks of data collection could be reduced to half a day, putting meta-learning within reach of our robotic arms. Off-policy learning offers further benefits beyond better sample efficiency when training from scratch. We could also make use of previously collected static datasets, and leverage data from other robots in other locations.

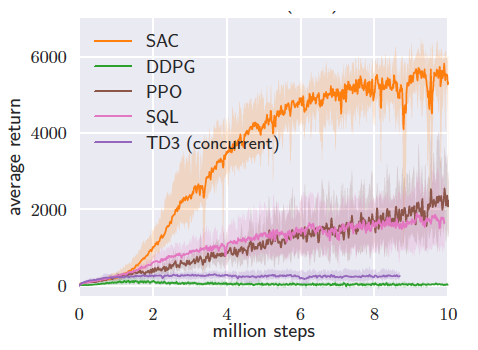
Off-policy RL (SAC) is more sample efficient than on-policy approaches (PPO) by 1-2 orders of magnitude (PPO eventually nears SAC performance), figure from Haarnoja et al. 2018.

The exploration problem

In supervised meta-learning, the data used to adapt in a new task is given. For example, in few-shot image classification, we provide the meta-learner with images and labels for the new classes we wish it to label. In RL, the agent is responsible for exploring and collecting its own data, so the adaptation procedure must include efficient exploration strategies. Black-box meta-learners (RL2, Wang et al., and SNAIL) can learn these exploration strategies as the entire adaptation procedure is treated as one long sequence in the recurrent optimization. Similarly, gradient-based meta-RL approaches can meta-learn exploration strategies by assigning credit to the trajectories collected by the pre-update policy to returns earned by the post-update policy (see Rothfuss et al.). While the capability exists, in practice these methods don’t learn temporally-extended exploration strategies.

To remedy this issue, MAESN adds structured stochasticity in the form of probabilistic latent variables which condition the policy, and which are adapted via gradient descent to a new task. The model is trained so that samples from the prior encode exploration trajectories, while samples from the adapted variables result in optimal adapted trajectories. Broadly, all these schemes work with on-policy RL algorithms because they rely on the exploration and adapted trajectories being sampled from the same current policy, hence requiring on-policy sampling. To build an off-policy meta-RL algorithm, we will take a different approach to exploration.

Exploration via meta-learned posterior sampling

One very intuitive way to explore in a new scenario is to pretend that it’s one you’ve already seen. For example, if you discover a pitaya (dragon fruit) for the first time and want to eat it, you might follow your policy for eating mangoes and decide to slice the fruit with a knife. This is certainly a good exploration strategy that leads you to the delicious speckled flesh inside. Since the flesh looks and feels much more like a kiwi than a mango, you might then switch to your kiwi-eating policy and grab a spoon to dig out the treat.

In the RL literature, this method of exploration is called posterior sampling (or Thompson sampling). The agent maintains a distribution over MDPs, then iteratively samples an MDP from this distribution, acts optimally according to it, and updates the distribution with the collected evidence. As more data is collected, the posterior distribution narrows, providing a smooth transition between exploration and exploitation. This strategy may seem limited because it precludes the possibility of taking purely exploratory actions; however, prior work has established that the worst-case cumulative regret guaranteed by posterior sampling is close that of state of the art exploration strategies.

Eating a strange new fruit via posterior sampling.

Turning to practical concerns, how do we represent this distribution over MDPs? One possibility is to maintain distributions over the transition and reward functions. To act according to the sampled model, we can use any model-based RL algorithm. Bootstrapped DQN applies this idea to the model-free deep RL setting, and maintains an approximate posterior over Q-functions. Our insight is that we can extend this idea to the multi-task setting by learning a distribution over Q-functions for different tasks, and that this distribution is useful for exploring in new related tasks.

To enable posterior sampling in meta-RL, we will model our distribution over MDPs as a distribution over Q-functions. We instantiate latent variables $z$, inferred from experience (or context), that the Q-function will take as input to modulate its predictions. During meta-training, the prior over $z$ is learned to represent the meta-training task distribution. Faced with a new task at test-time, the agent samples a hypothesis from the prior, takes actions in the environment according to this hypothesis, and then updates the posterior with the new evidence. As the agent collects trajectories, the posterior narrows as the agent gains a better guess for the current task.

Meta-RL as a POMDP

This Bayesian perspective on meta-RL illuminates the relationship between meta-RL and partially observed MDPs (POMDPs). POMDPs are useful for modeling situations in which your current observation doesn’t tell you everything about the current state (in other words, the current state is only partially observed). For example, if you’re walking around a building and the lights go out, you can’t tell from your immediate observation of darkness where you are. Solving POMDPs involves integrating information over a history of observations in order to accurately estimate the current state. In the dark building, you would still have a guess for your position because you can remember what you saw before the lights went out.

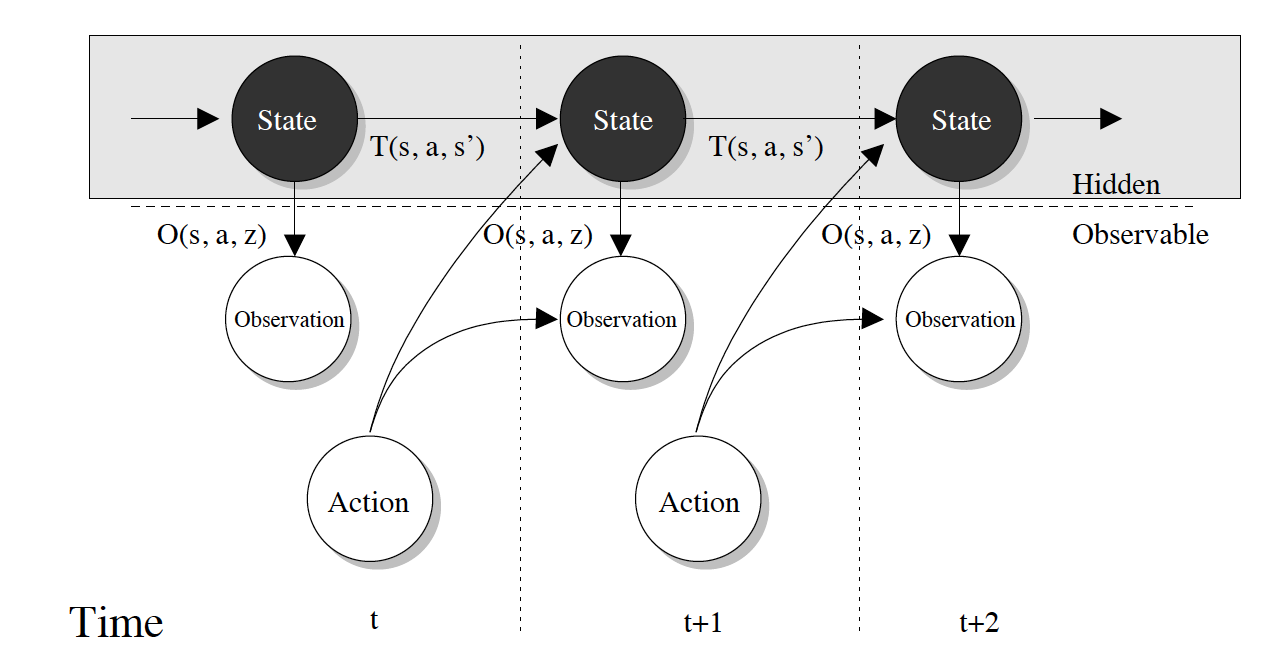
The graphical model of a POMDP, figure from Roy 2003

Meta-RL can be viewed as a POMDP with the special structure that the task is the only unobserved part of the state. In our example, the task might be finding an office you’ve never been to. In a general POMDP, the state must be re-estimated at each time step — you constantly update your estimate of where you are in the building every time you move. In the meta-RL case, the task remains constant across trajectories — in our non-magical world, the location of the office doesn’t change as you look for it. This means we can maintain an estimate of the location of the office without worrying about underlying system dynamics changing its location at every time step. Casting our meta-RL algorithm into the parlance of POMDPs, we maintain a belief state over the task, which we update as we collect evidence over multiple trajectories.

PEARL in a (sea)shell

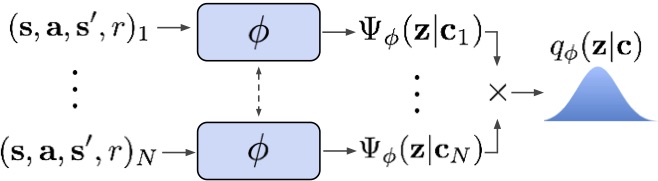
How can we integrate a belief over the task with existing off-policy RL algorithms? To start, we can infer a variational approximation to the posterior belief with an encoder network $q_\phi(z | c)$ that takes context (experience) as input. To keep things tractable, we’ll represent the posterior as a Gaussian. For the RL agent, we choose to build on Soft Actor-Critic (SAC) because of its state-of-the-art performance and sample efficiency. Samples from the belief are passed to the actor and critic so they can make predictions according to the sampled task. Meta-training then consists of learning to infer the posterior $q_\phi(z | c)$ given context, and training the actor and critic to act optimally according to a given $z$. The encoder is optimized with gradients from the critic (so that $q_\phi(z | c)$ represents a distribution over Q-functions), as well as an information bottleneck. This bottleneck appears as a consequence of deriving the variational lower bound, but it can also be interpreted intuitively as minimizing the information between the context and $z$ so that $z$ contains the minimum information needed to predict state-action values.

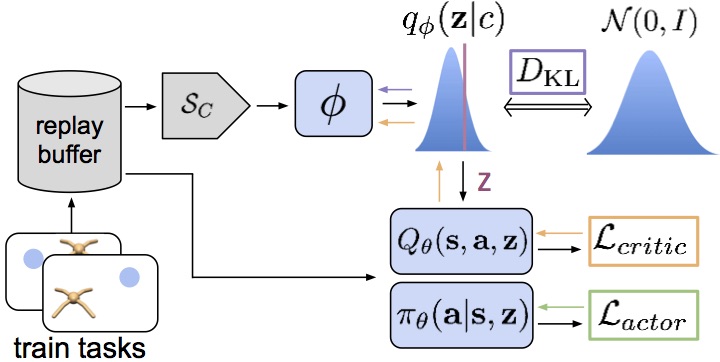
One thing to note about this scheme is that the batches of data sampled to train the actor and critic can be separate from the batches of context. Intuitively this makes sense — by explicitly representing a belief over the task, the agent disentangles task inference from control, and can use completely different data sources to learn each. This is in contrast to methods like MAML and RL2 which entangle task inference and control and must thus use one batch of data for both.

This disentanglement turns out to be important for off-policy meta-training. To understand why, consider that modern meta-learning is predicated on the assumption that train and test time should match. For example, a meta-learner tasked with classifying new animal species at test time should be trained on a distribution of classes that includes animals. The analogy to this in RL is that if at test time the agent will adapt by gathering on-policy data, it should be trained with on-policy data as well. Using off-policy data during training thus presents a distribution shift that undermines this foundational assumption. In PEARL, we can mitigate this distribution shift while still using largely off-policy data by sampling on-policy data for the context, while using off-policy data for the actor-critic training.

One part of the algorithm that remains abstract at this point is the encoder architecture. Recall that the encoder’s job is to take in context (a set of transitions consisting of states, actions, rewards, and next states) and produce the parameters of a Gaussian posterior over the latent context variables. While a recurrent network might seem like the obvious choice here, we note that the Markov property implies that the transitions can be encoded without regard for their order in the trajectory. With this observation in mind, we employ a permutation-invariant encoder that predicts a Gaussian factor for each transition independently, and take the product of these factors to form the posterior. Compared to an RNN, this architecture is faster and more stable to optimize, and can accommodate much larger contexts.

Enough already, does it work?

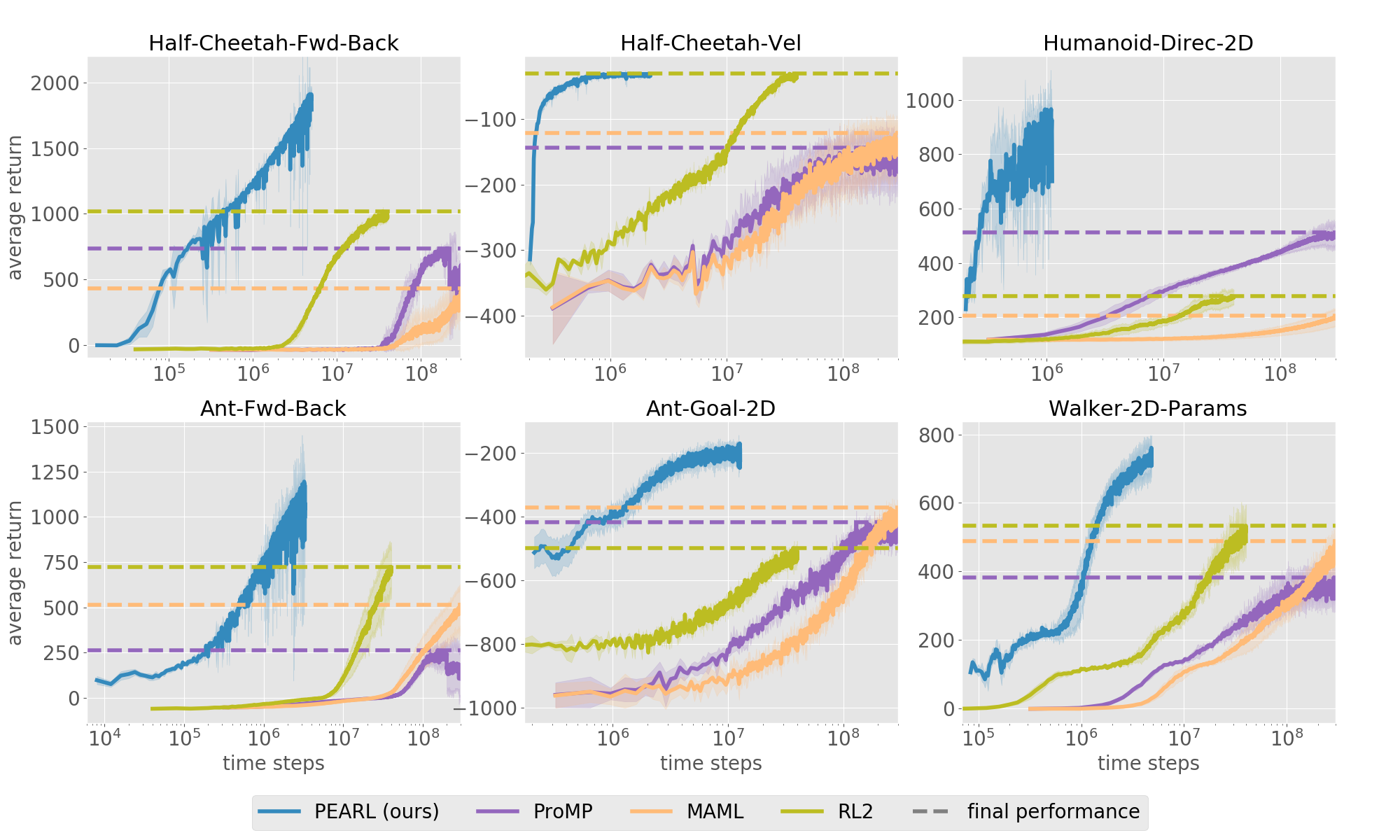
We tested PEARL on six benchmark continuous control domains using the MuJoCo simulator that vary reward or dynamics functions across tasks. For example, for the Ant agent different tasks correspond to navigating to different goal positions on the 2D plane (bottom center), while for the Walker agent tasks correspond to different parameters of its joints and other physical parameters (bottom right). We compared PEARL to three state-of-the-art meta-RL algorithms: ProMP, MAML, and RL2. Our results are plotted below, with PEARL in blue. Note that the x-axis is in log scale. By leveraging off-policy data during meta-training, our approach improves sample efficiency by 20-100X across the board. It also regularly outperforms the baselines in terms of final performance.

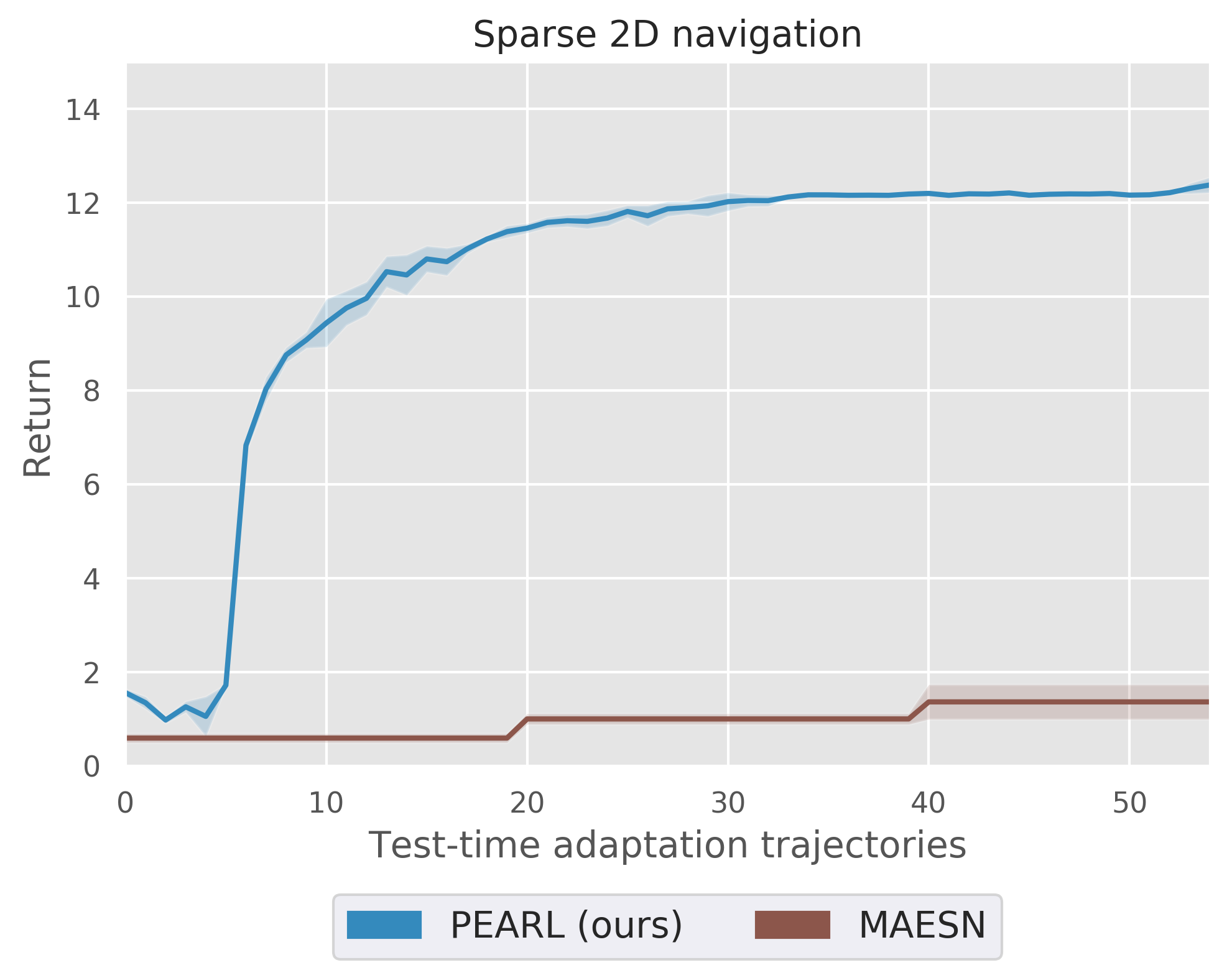
Efficient exploration is particularly important in sparse reward domains. Consider a point robot that must navigate to different goal locations on a half-circle, and receives a reward only when within a small radius of the goal (visualized in blue). By sampling different hypotheses for the goal location and subsequently updating its belief, the agent efficiently explores until it finds the goal. We compared PEARL to MAESN, which as we discussed earlier meta-learns exploration strategies via latent variables, and found that PEARL explores more effectively, in addition to being more sample efficient during meta-training.

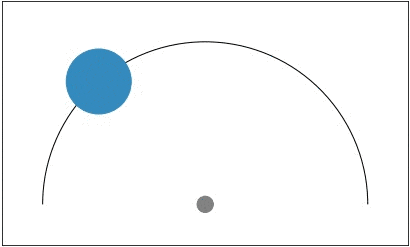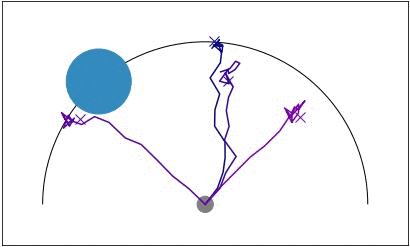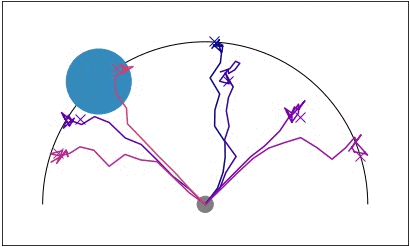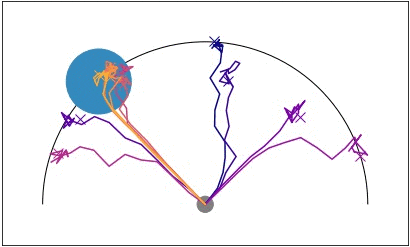
Point robot uses posterior sampling to explore and find the goal in a sparse reward setting.

Future Directions

While meta-learning provides a potential solution for how agents can quickly adapt to new scenarios, it has inevitably created more questions! For example, where do the meta-training tasks come from — must they be hand-designed or can they be automatically generated? While meta-learning is episodic by nature, the real world is a continuous never-ending stream — how do agents deal with tasks that change over time? Reward functions are fiendishly difficult to design — instead, can we leverage binary feedback, preferences, and demonstrations together in our meta-RL algorithms? We hope the Bayesian inference aspect of PEARL provides a new perspective on tackling some of these problems, and that PEARL’s ability to learn off-policy is a first step towards meta-RL that scales to real systems.

We would like to thank Sergey Levine, Chelsea Finn, and Ignasi Clavera for their helpful feedback on this post.

Much of this post was based on the following research paper:

• Efficient Off-Policy Meta-RL via Probabilistic Context Variables
  Kate Rakelly*, Aurick Zhou*, Deirdre Quillen, Chelsea Finn, Sergey Levine. In ICML, 2019.