The Confluence of Geometry and Learning

Shubham Tulsiani and Tinghui Zhou    Jul 11, 2017

Given only a single 2D image, humans are able to effortlessly infer the rich 3D structure of the underlying scene. Since inferring 3D from 2D is an ambiguous task by itself (see e.g. the left figure below), we must rely on learning from our past visual experiences. These visual experiences solely consist of 2D projections (as received on the retina) of the 3D world. Therefore, the learning signal for our 3D perception capability likely comes from making consistent connections among different perspectives of the world that only capture partial evidence of the 3D reality. We present methods for building 3D prediction systems that can learn in a similar manner.

sinha MVS sampleres
An image could be the projection of infinitely many 3D structures (figure from Sinha & Adelson). Our visual experiences solely comprise of 2D projections of the 3D world. Our approach can learn from 2D projections and predict shape (top) or depth (bottom) from a single image.

Building computational models for single image 3D inference is a long-standing problem in computer vision. Early attempts, such as the Blocks World or 3D surface from line drawings, leveraged explicit reasoning over geometric cues to optimize for the 3D structure. Over the years, the incorporation of supervised learning allowed approaches to scale to more realistic settings and infer qualitative (e.g. Hoiem et al.) or quantitative (e.g. Saxena et al.) 3D representations. The trend of obtaining impressive results in realistic settings has since continued to the current CNN-based incarnations (e.g. Eigen & Fergus, Wang et al.), but at the cost of increasing reliance on direct 3D supervision, making this paradigm rather restrictive. It is costly and painstaking, if not impossible, to obtain such supervision at a large scale. Instead, akin to the human visual system, we want our computational systems to learn 3D prediction without requiring 3D supervision.

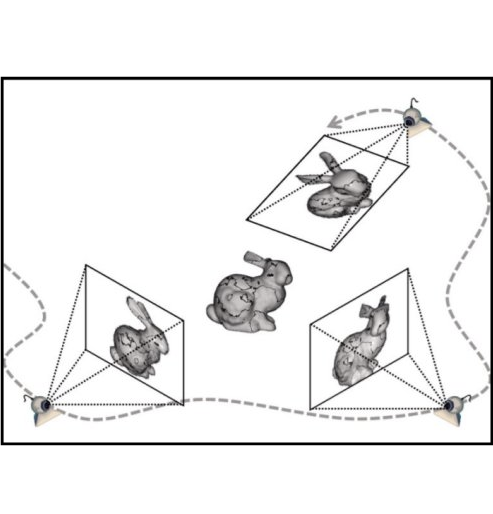
With this goal in mind, our work and several other recent approaches explore another form of supervision: multi-view observations, for learning single-view 3D. Interestingly, not only do these different works share the goal of incorporating multi-view supervision, the methodologies used also follow common principles. A unifying foundation to these approaches is the interaction between learning and geometry, where predictions made by the learning system are encouraged to be ‘geometrically consistent’ with the multi-view observations. Therefore, geometry acts as a bridge between the learning system and the multi-view training data.

Learning via Geometric Consistency

Our aim is to to learn a Predictor $P$ (typically a neural network) that can infer 3D from a single 2D image. Under the supervision setting considered, the training data consists of multiple observations from different viewpoints. As alluded to earlier, geometry acts as a bridge to allow learning the Predictor $P$ using the training data. This is because we know precisely, in the form of concise geometric equations, the relationship between a 3D representation and the corresponding 2D projections. We can therefore train $P$ to predict 3D that is geometrically consistent with the associated 2D observations.

geometric consistency

To illustrate the training process, consider a simple game between the Predictor $P$ and a geometry expert, the Verifier $V$. We give $P$ a single image $I$, and it predicts a 3D shape $S$. $V$, who is then given the prediction $S$, and an observation $O$ of the world from a different camera viewpoint $C$, uses the geometric equations to validate if these are consistent. We ask $P$ to predict $S$ that would pass this consistency check performed by $V$. The key insight is that since $P$ does not know $(O, C)$ which will be used to verify its prediction, it will have to predict $S$ that is consistent will all the possible observations (similar to the unknown ground-truth $S_{gt}$). This allows us to define the following training algorithm to learn 3D-from-2D prediction using only multi-view supervision.

  • Pick a random training image $I$ with associated observation $O$ from viewpoint $C$.
  • Predict $S = P(I)$. Use $V$ to check consistency between $(S, O, C)$
  • Update $P$, using gradient descent, to make $S$ more consistent with $(O, C)$.
  • Repeat until convergence.

The recent approaches pursuing single-view prediction using multi-view supervision all adhere to this template, the differences being the form of 3D prediction being pursued (e.g. depth or shape), and the kinds of multi-view observations needed (e.g. color images or foreground masks). We now look at two papers which push the boundaries of the multi-view supervision paradigm. The first one leverages classical ray consistency formulations to introduce a generic Verifier which can measure consistency between a 3D shape and diverse kinds of observations $O$. The second one demonstrates that it is possible to even further relax the supervision required and presents a technique to learn 3D-from-2D without even requiring the camera viewpoints $C$ for training.

Differentiable Ray Consistency

In our recent paper, we formulate a Verifier $V$ to measure the consistency between a 3D shape (represented as a probabilistic occupancy grid) and a 2D observation. Our generic formulation allows learning volumetric 3D prediction by leveraging different types of multi-view observations e.g. foreground masks, depth, color images, semantics etc. as supervision.

An insight which allows defining $V$ is that each pixel in the observation $O$ corresponds to a ray with some associated information. Then, instead of computing the geometric consistency between the observation $O$ and the shape $S$, we can consider, one ray at a time, the consistency between the shape $S$ and a ray $r$.

rays

The figure above depicts the various aspects of formulating the ray consistency cost. a) The predicted 3D shape and a sample ray with which we measure consistency. b,c) We trace the ray through the 3D shape and compute event probabilities - the probabilities that the ray terminates at various points on its path. d) We can measure how inconsistent each ray termination event is with the information available for that ray. e) By defining the ray consistency cost as the expected event cost, we can compute gradients for how the prediction should be updated to increase the consistency. While in this example we visualize a depth observation $O$, an advantage of our formulation is that it allows incorporating diverse kinds of observations (color images, foreground masks etc.) by simply defining the corresponding event cost function.

The results of 3D-from-2D prediction learned using our framework in different settings are shown below. Note that all the visualized predictions are obtained from a single RGB image by a Predictor $P$ trained without using 3D supervision.
Results on ShapeNet dataset using multiple depth images as supervision for training. a) Input image. b,c) Predicted 3D shape. Results on PASCAL VOC dataset using pose and foreground masks as supervision for training. a) Input image. b,c) Predicted 3D shape.
Results on Cityscapes dataset using depth, semantics as supervision. a) Input image. b,c) Predicted 3D shape rendered under simulated forward motion. Results on ShapeNet dataset using multiple color images as supervision for training shape and per-voxel color prediction. a) Input image. b,c) Predicted 3D shape.

Learning Depth and Pose from Unlabeled Videos

Notice that in the above work, the input to the Verifier $V$ is an observation with known camera viewpoint/pose. This is reasonable from the perspective of an agent with sensorimotor functionality (e.g. human or robots with odometers), but prevents its applications to more unstructured data sources (e.g. videos). In another recent work, we show that the pose requirement can be relaxed, and in fact jointly learned with the single image 3D predictor $P$.

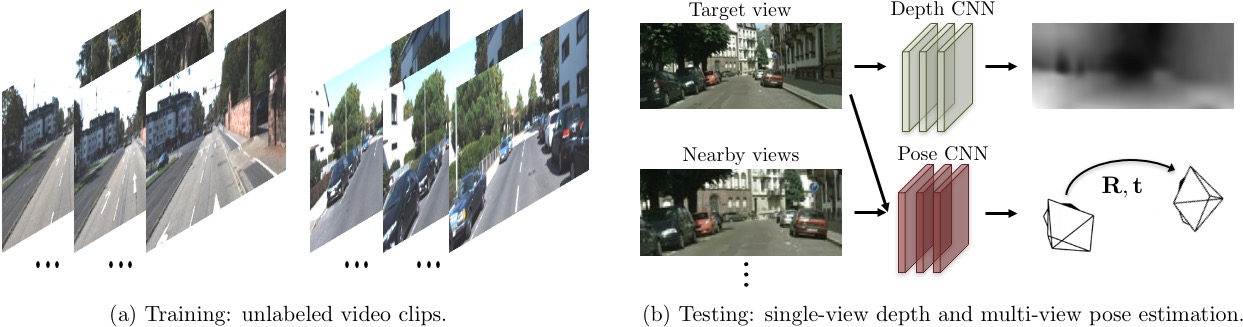
problem setup

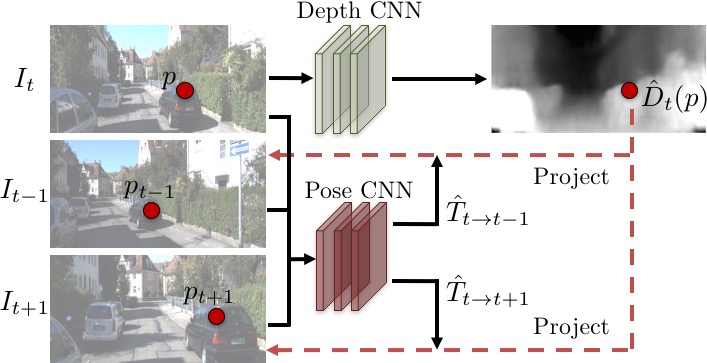
More specifically, our Verifier $V$ in this case is based on a differentiable depth-based view synthesizer that outputs a target view of the scene using the predicted depth map and pixels from a source view (i.e. observation) seen under a different camera pose. Here both the depth map and the camera pose are predicted, and the consistency is defined by the pixel reconstruction error between the synthesized and the ground-truth target view. By jointly learning the scene geometry and the camera pose, we are able to train the system on unlabeled video clips without any direct supervision for either depth or pose.

Training pipeline
Formulating the Verifier as a depth-based view synthesizer and joint learning of depth and camera pose allows us to train the entire system from unlabeled videos without any direct supervision for either depth or pose.

We train and evaluate our model on the KITTI and Cityscapes datasets, which consist of videos captured by a car driving in urban cities. The video below shows frame-by-frame (i.e. no temporal smoothness) prediction made by our single-view depth network (more can be found in the project webage).

depth_gif

Surprisingly, despite being trained without any ground-truth labels, our single-view depth model performs on par with some of the supervised baselines, while the pose estimation model is also comparable with well-established SLAM systems (see the paper for more details).

Learning single image 3D without 3D supervision is an exciting and thriving topic in computer vision. Using geometry as a bridge between the learning system and the multi-view training data allows us to bypass the tedious and expensive process of acquiring ground-truth 3D labels. More broadly, one could interpret the geometric consistency as a form of meta supervision on not what the prediction is but how it should behave. We believe that similar principles could be applied to other problem domains where obtaining direct labels is difficult or infeasible.

We would like to thank TZ’s advisor and TZ’s advisor’s advisor for their valuable feedback.

This post is based on the following papers:

Other recent multi-view supervised 3D prediction approaches:

Subscribe to our RSS feed.

Comments