Consider looking at a photograph of a chair.
We humans have the remarkable capacity of inferring properties about the 3D shape of the chair from this single photograph even if we might not have seen such a chair ever before.
A more representative example of our experience though is being in the same physical space as the chair and accumulating information from various viewpoints around it to build up our hypothesis of the chair’s 3D shape.
How do we solve this complex 2D to 3D inference task? What kind of cues do we use?
How do we seamlessly integrate information from just a few views to build up a holistic 3D model of the scene?
A vast body of work in computer vision has been devoted to developing algorithms which leverage various cues from images that enable this task of 3D reconstruction. They range from monocular cues such as shading, linear perspective, size constancy etc. to binocular and even multi-view stereopsis. The dominant paradigm for integrating multiple views has been to leverage stereopsis, i.e. if a point in the 3D world is viewed from multiple viewpoints, its location in 3D can be determined by triangulating its projections in the respective views. This family of algorithms has led to work on Structure from Motion (SfM) and Multi-view Stereo (MVS) and have been used to produce city-scale 3D models and enable rich visual experiences such as 3D flyover maps. With the advent of deep neural networks and their immense power in modelling visual data, the focus has recently shifted to modelling monocular cues implicitly with a CNN and predicting 3D from a single image as depth/surface orientation maps or 3D voxel grids.
In our recent work, we tried to unify these paradigms of single and multi-view 3D reconstruction. We proposed a novel system called a Learnt Stereo Machine (LSM) that can leverage monocular/semantic cues for single-view 3D reconstruction while also being able to integrate information from multiple viewpoints using stereopsis - all within a single end-to-end learnt deep neural network.
Learnt Stereo Machines
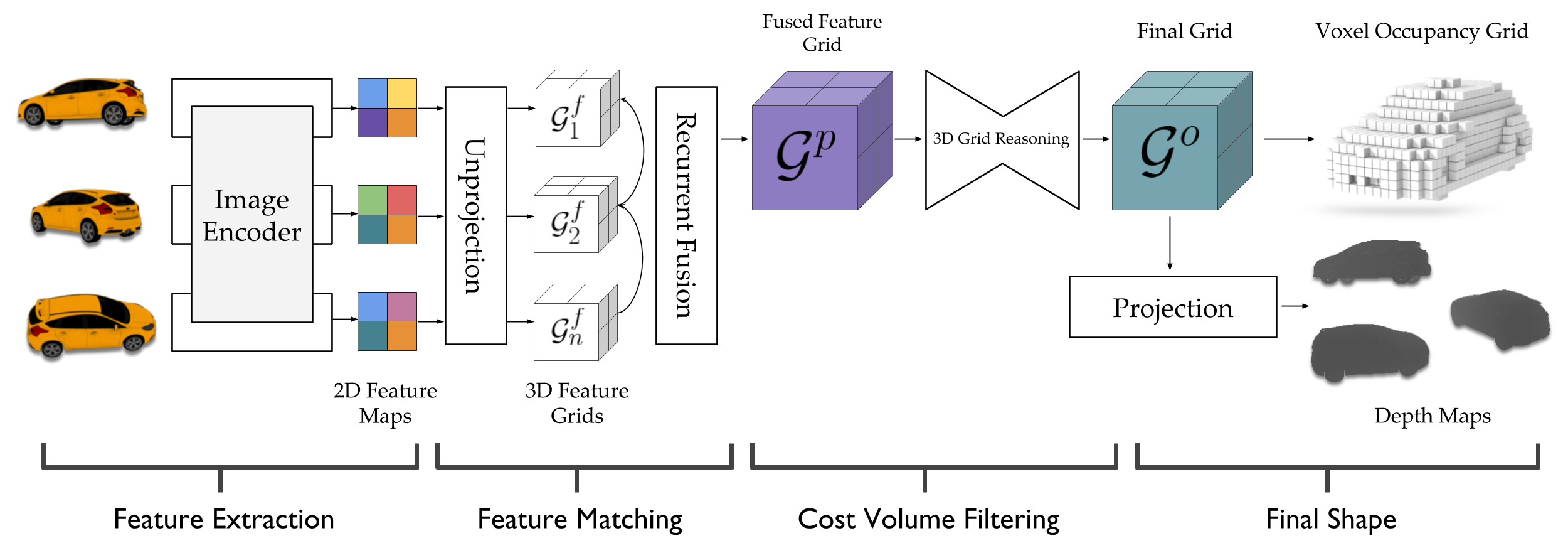
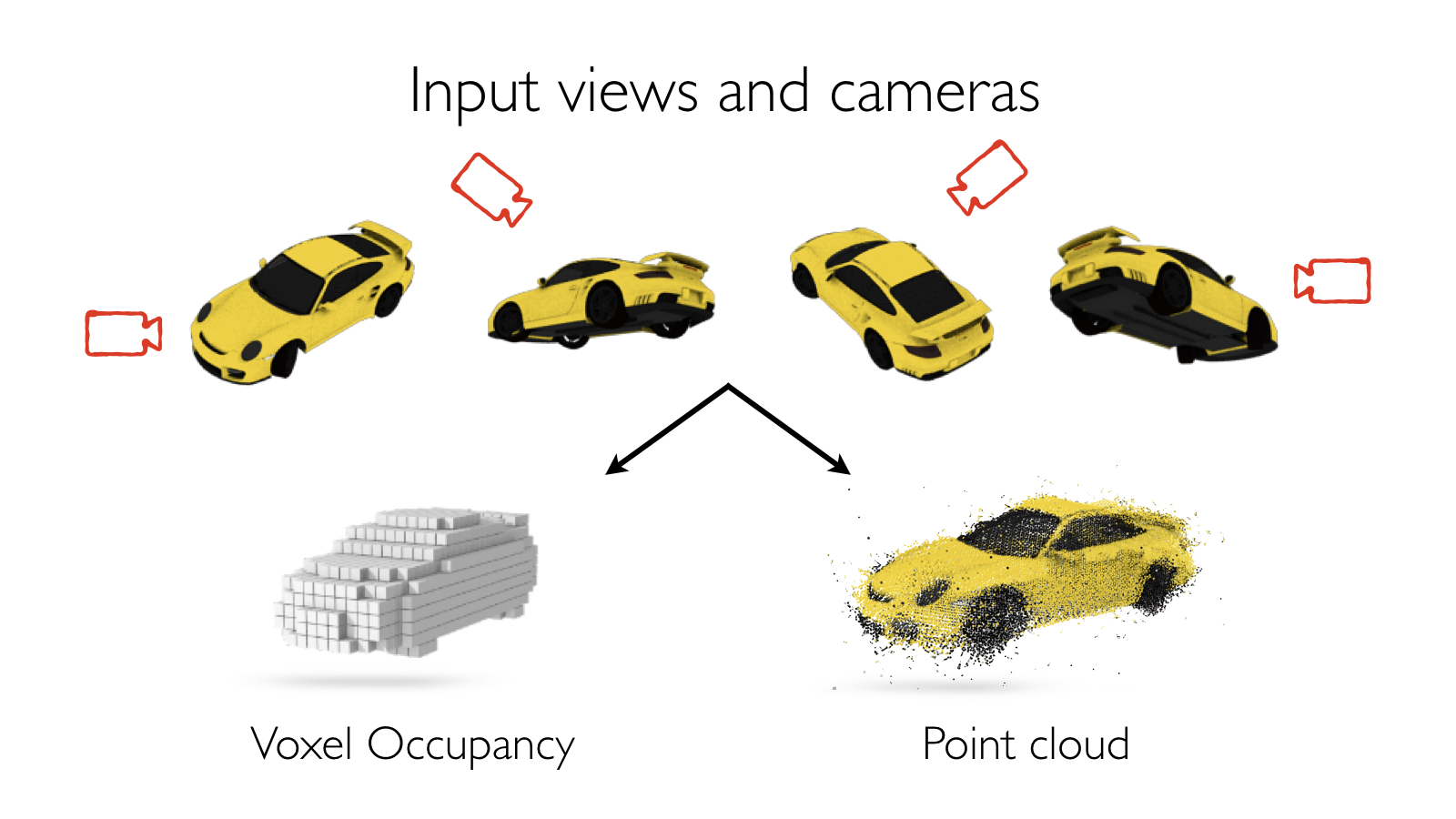
LSMs are designed to solve the task of multi-view stereo. Given a set of images with known camera poses, they produce a 3D model for the underlying scene - specifically either a voxel occupancy grid or a dense point cloud of the scene in the form of a pixel-wise depth map per input view. While designing LSMs, we drew inspiration from classic works on MVS. These methods first extract features from the images for finding correspondences between them. By comparing the features between images, a matching cost volume is formed. These (typically noisy) matching costs are then filtered/regularized by aggregating information across multiple scales and incorporating priors on shape such as local smoothness, piecewise planarity etc. The final filtered cost volume is then decoded into the desired shape representation such as a 3D volume/surface/disparity maps.
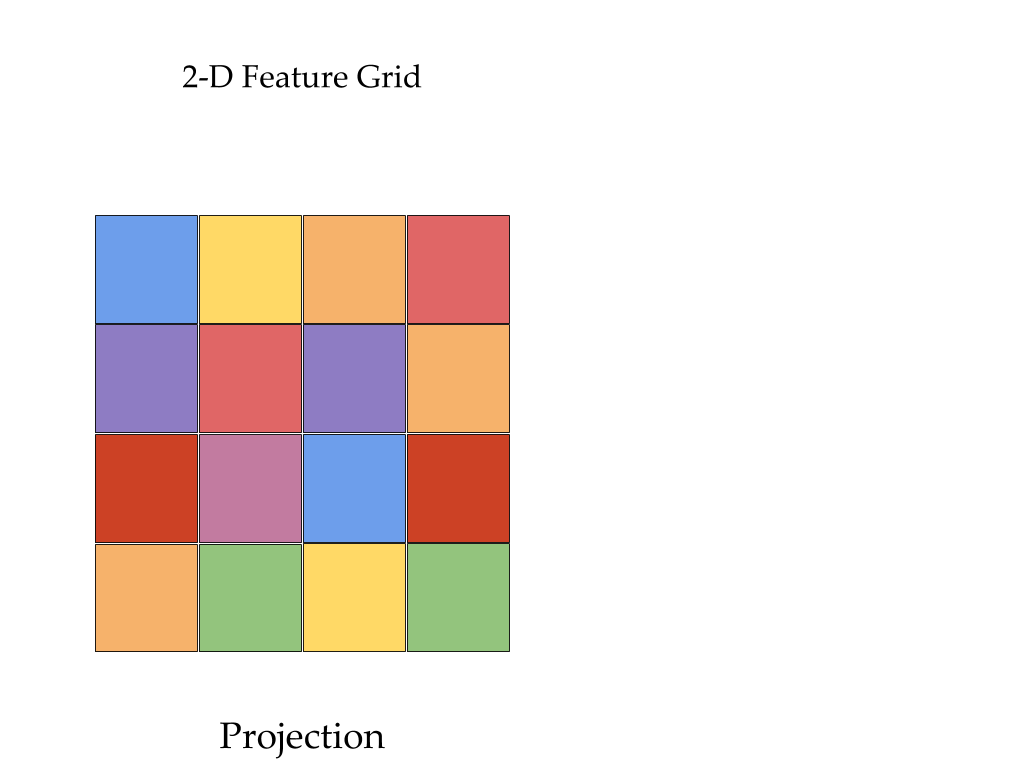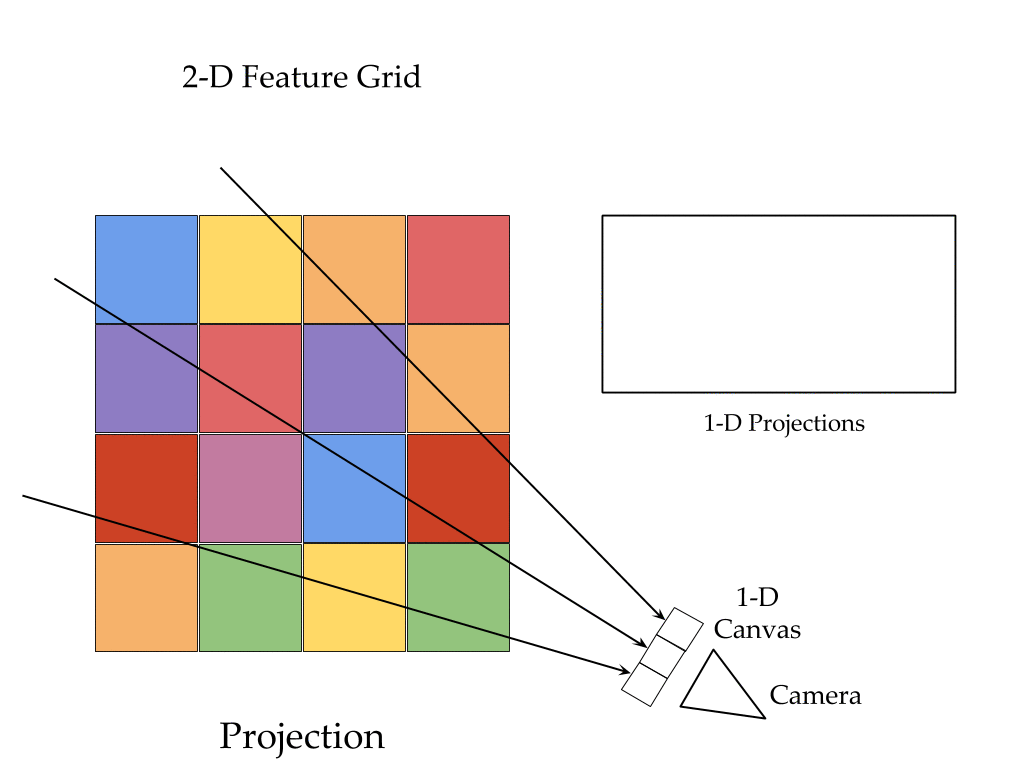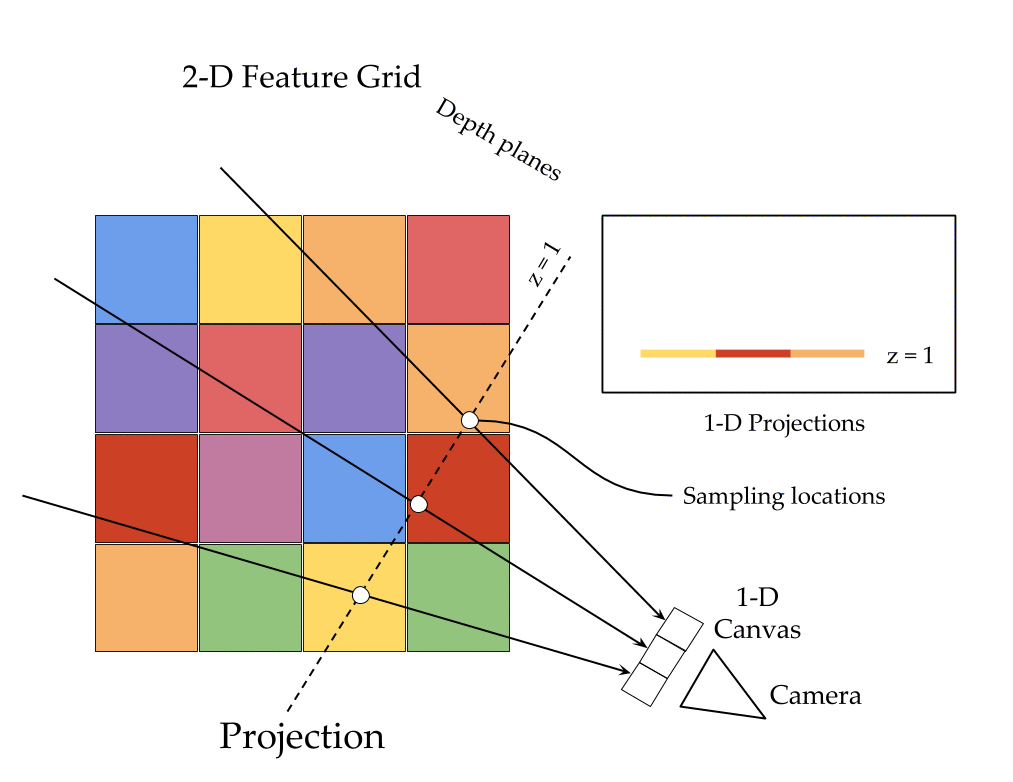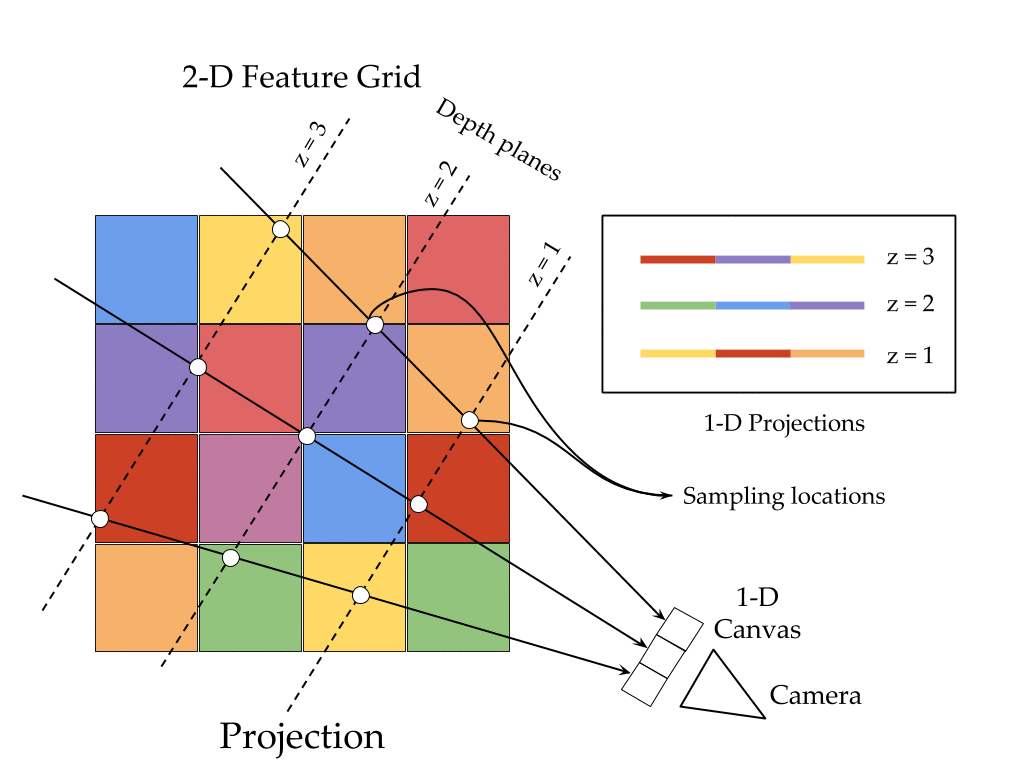
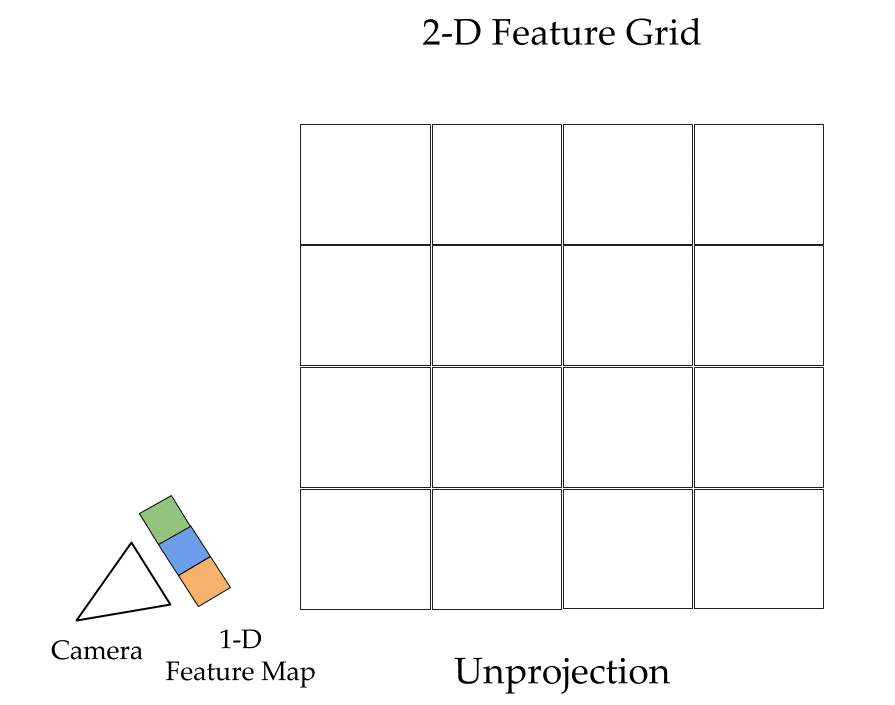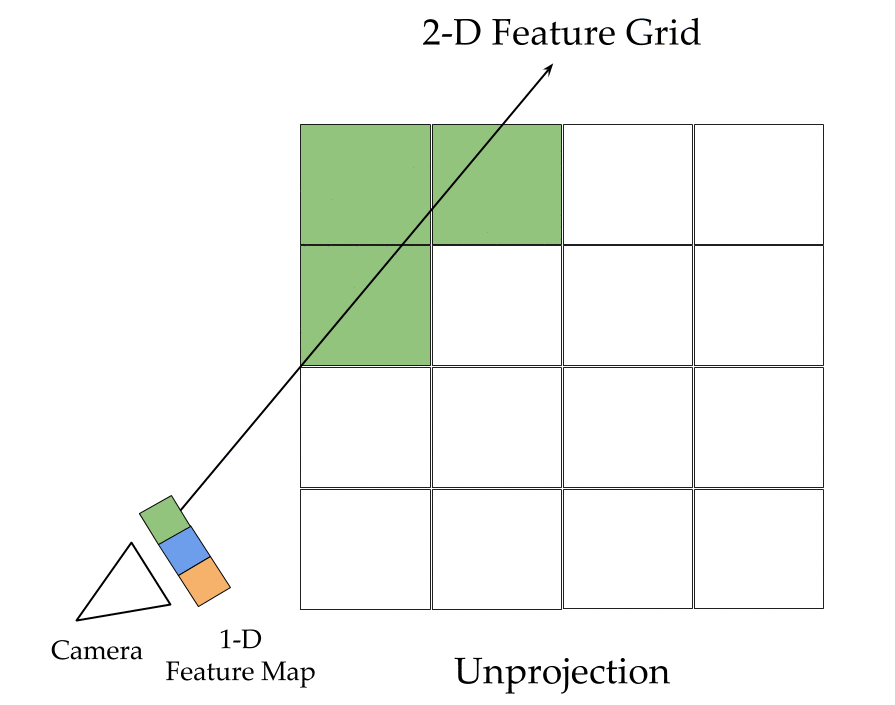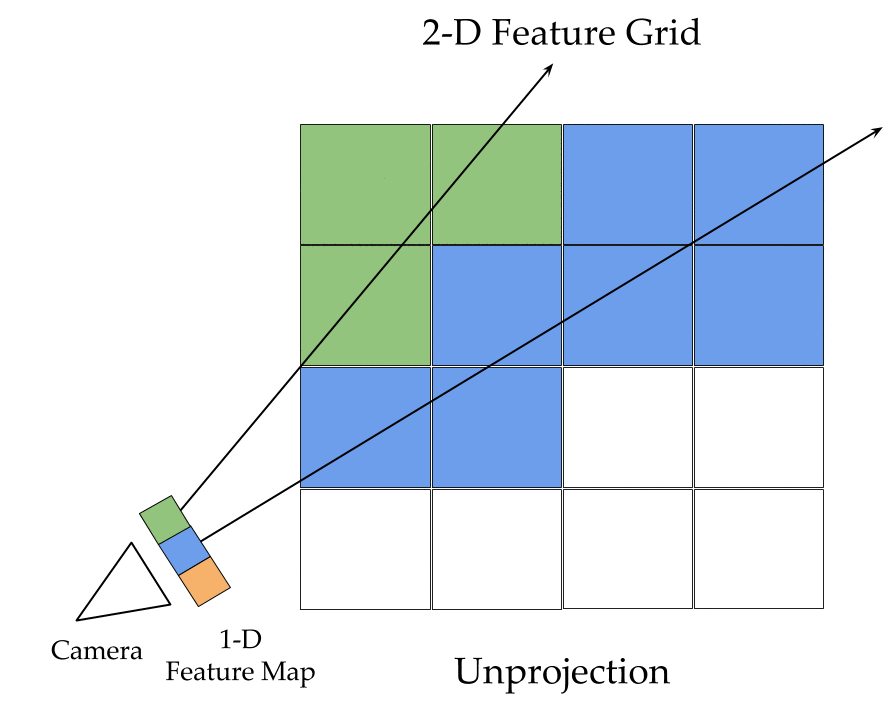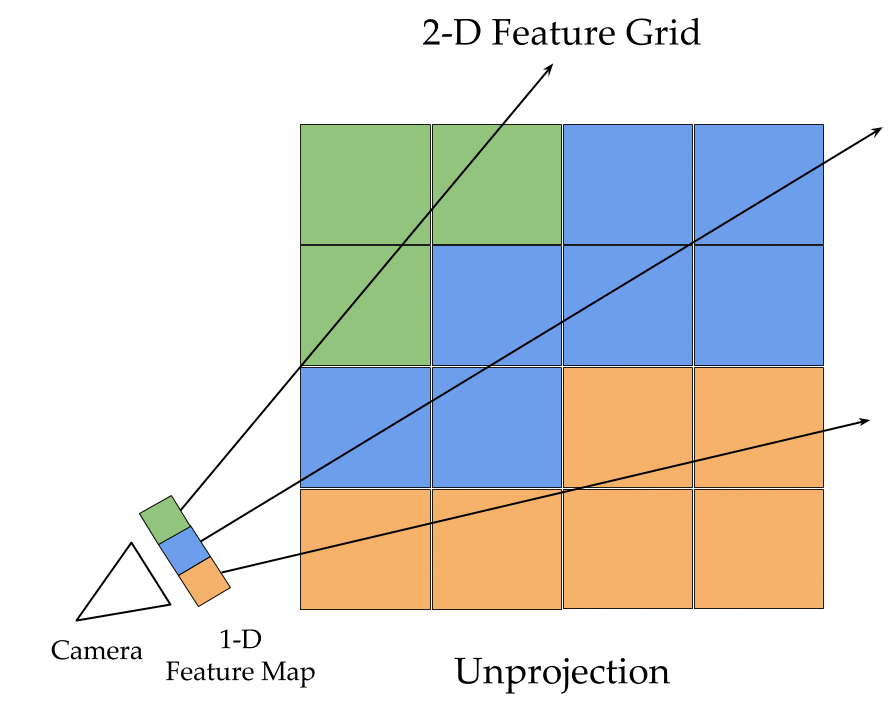
The key ingredients here are a differentiable feature projection and unprojection modules which allow LSMs to move between 2D image and 3D world spaces in a geometrically consistent manner. The unprojection operation places features from a 2D image (extracted by a feedforward CNN) into a 3D world grid such that features from multiple such images align in the 3D grid according to epipolar constraints. This simplifies feature matching as now a search along an epipolar line to compute matching costs reduces to just looking up all features which map to a given location in the 3D world grid. This feature matching is modeled using a 3D recurrent unit which performs sequential matching of the unprojected grids while maintaining a running estimate of the matching scores. Once we filter the local matching cost volume using a 3D CNN, we either decode it directly into a 3D voxel occupancy grid for the voxel prediction task or project it back into 2D image space using a differentiable projection operation. The projection operation can be thought of as the inverse of the unprojection operation where we take a 3D feature grid and sample features along viewing rays at equal depth intervals to place them in a 2D feature map. These projected feature maps are then decoded into per view depth maps by a series of convolution operations. As every step in our network is completely differentiable, we can train the system end-to-end with depth maps or voxel grids as supervision!
As LSMs can predict 3D from a variable number of images (even just a single image), they can choose to either rely heavily on multi-view stereopsis cues or single-view semantic cues depending on the instance and number of views at hand. LSMs can produce both coarse full 3D voxel grids as well as dense depth maps thus unifying the two major paradigms in 3D prediction using deep neural networks.
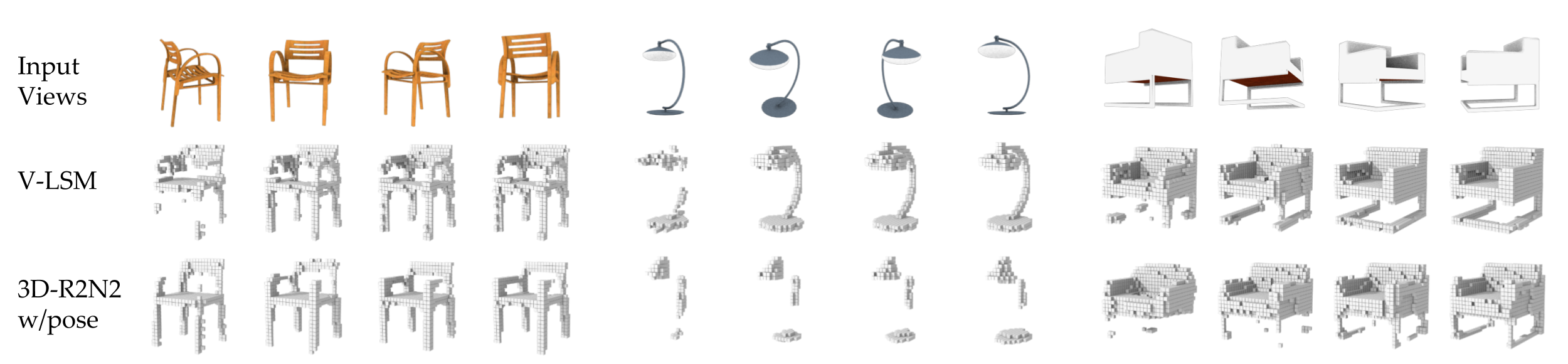
In our report, we showed drastic improvements on voxel based multi-view 3D object reconstruction when compared to the previous state-of-the-art which integrates multiple views using a recurrent neural network. We also demonstrated out-of-category generalization, i.e. LSMs can reconstruct cars even if they are only trained on images of aeroplanes and chairs. This is only possible due to our geometric treatment of the task. We also show dense reconstructions from a few views - much fewer than what is required by classical MVS systems.

What’s Next?
LSMs are a step towards unifying a number of paradigms in 3D reconstruction - single and multi-view, semantic and geometric reconstruction, coarse and dense predictions. A joint treatment of these problems helps us learn models that are more robust and accurate while also being simpler to deploy than pipelined solutions.
These are exciting times in 3D computer vision. Predicting high resolution geometry with deep networks is now possible. We can even train for 3D prediction without explicit 3D supervision. We can’t wait to use these techniques/ideas within LSMs. It remains to be seen how lifting images from 2D to 3D and reasoning about them in metric world space would help other downstream tasks such as navigation and grasping but it sure will be an interesting journey! We will release the code for LSMs soon for easy experimentation and reproducibility. Feel free to use it and leave comments!
We would like to thank Saurabh Gupta, Shubham Tulsiani and David Fouhey.
This blog post is based on the following report
