(Joint work with Ronghang Hu, Marcus Rohrbach, Trevor Darrell, Dan Klein and Kate Saenko.)

Suppose we’re building a household robot, and want it to be able to answer questions about its surroundings. We might ask questions like these:

How can we ensure that the robot can answer these questions correctly? The standard approach in deep learning is to collect a large dataset of questions, images, and answers, and train a single neural network to map directly from questions and images to answers. If most questions look like the one on the left, we have a familiar image recognition problem, and these kinds of monolithic approaches are quite effective:

But things don’t work quite so well for questions like the one on the right:

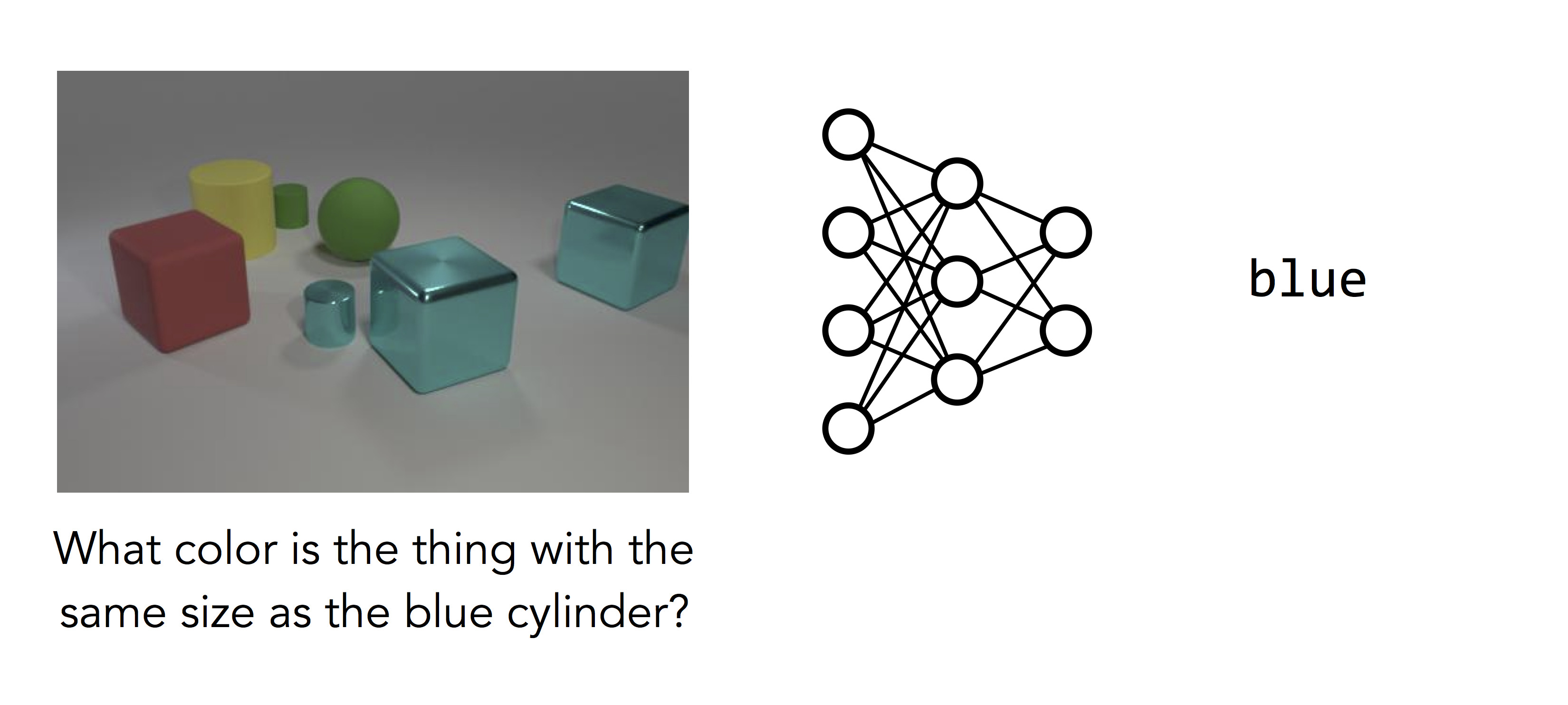
Here the network we trained has given up and guessed the most common color in the image. What makes this question so much harder? Even though the image is cleaner, the question requires many steps of reasoning: rather than simply recognizing the main object in the image, the model must first find the blue cylinder, locate the other object with the same size, and then determine its color. This is a complicated computation, and it’s a computation specific to the question that was asked. Different questions require different sequences of steps to solve.

The dominant paradigm in deep learning is a "one size fits all" approach: for whatever problem we’re trying to solve, we write down a fixed model architecture that we hope can capture everything about the relationship between the input and output, and learn parameters for that fixed model from labeled training data.

But real-world reasoning doesn’t work this way: it involves a variety of different capabilities, combined and synthesized in new ways for every new challenge we encounter in the wild. What we need is a model that can dynamically determine how to reason about the problem in front of it—a network that can choose its own structure on the fly. In this post, we’ll talk about a new class of models we call neural module networks (NMNs), which incorporate this more flexible approach to problem-solving while preserving the expressive power that makes deep learning so effective.

Earlier, we noticed that there are three different steps involved in answering the question above: finding a blue cylinder, finding something else the same size, and determining its color. We can draw this schematically like:

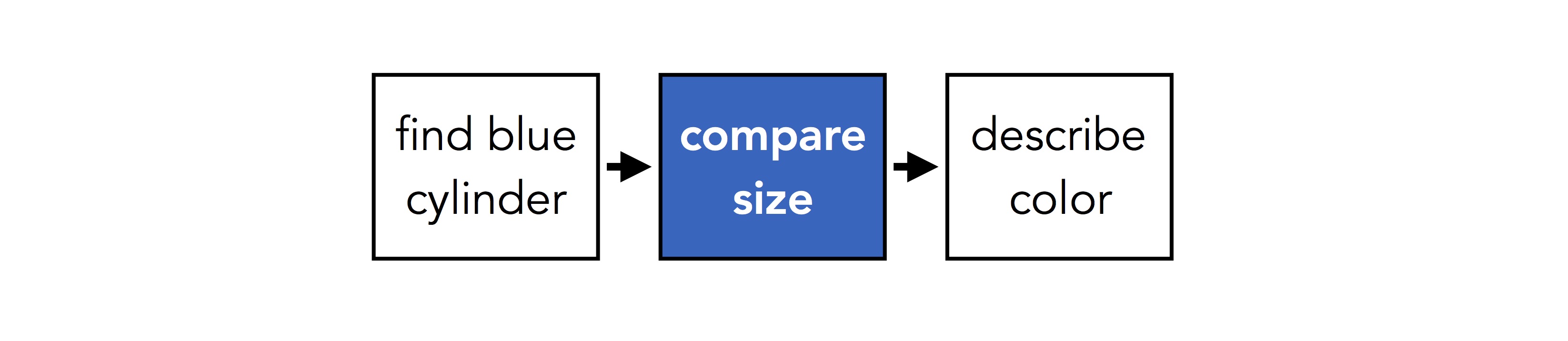
A different question might involve a different series of steps. If we ask "how many things are the same size as the ball?", we might have something like:

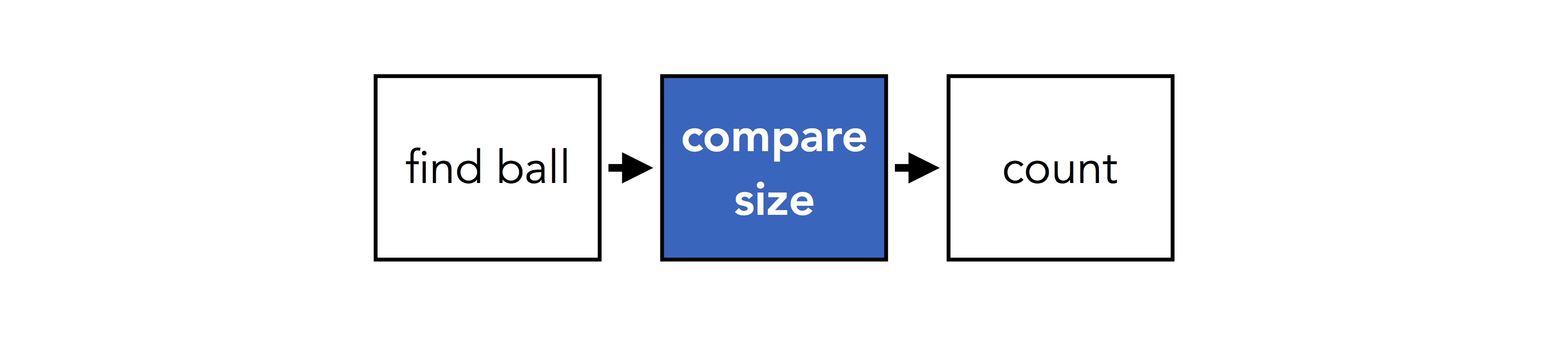
Basic operations like "compare size" are shared between questions, but they get used in different ways. The key idea behind NMNs is to make this sharing explicit: we use two different network structures to answer the two questions above, but we share weights between pieces of networks that involve the same basic operations:

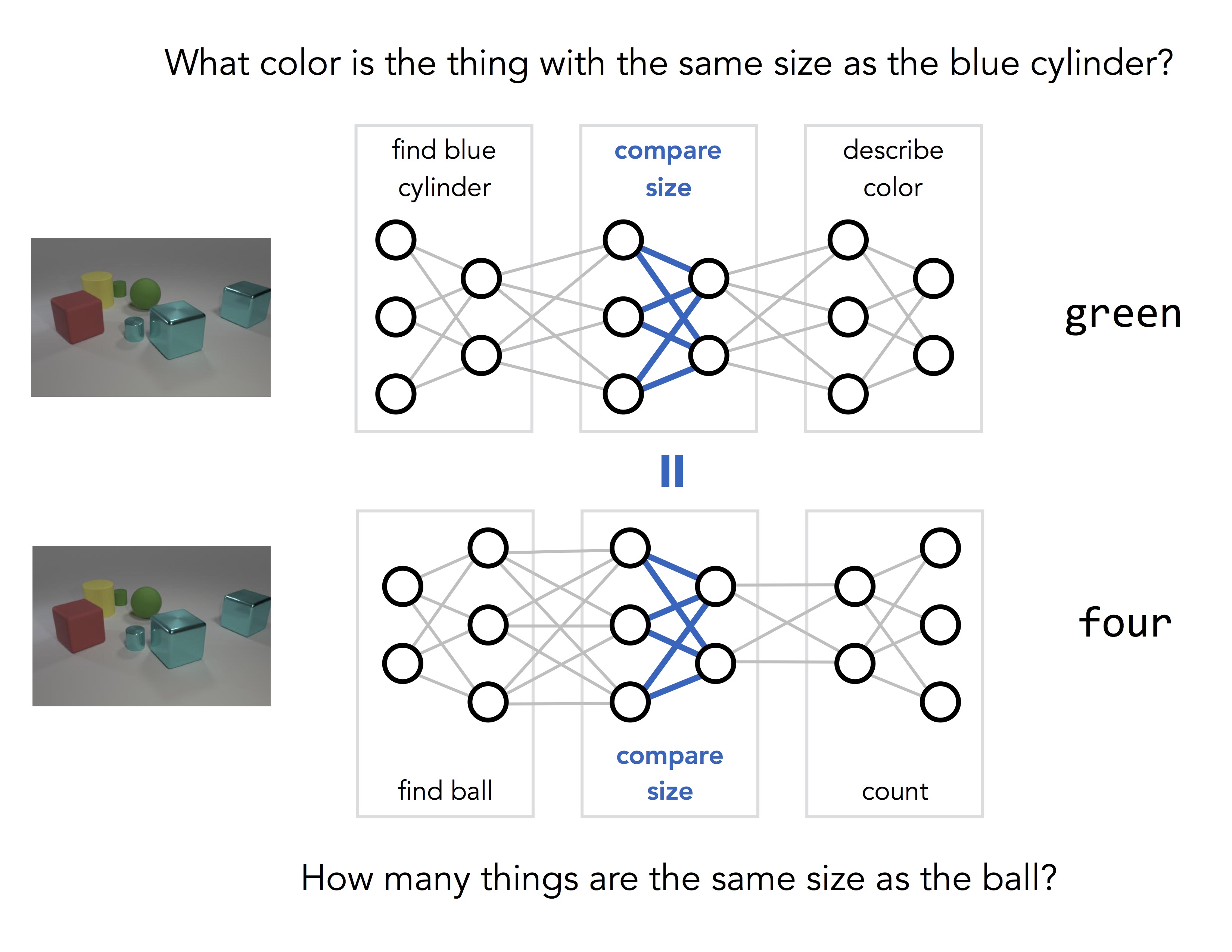
How do we learn a model like this? Rather than training a single large network on lots of input/output pairs, we actually train a huge number of different networks at the same time, while tying their parameters together where appropriate:

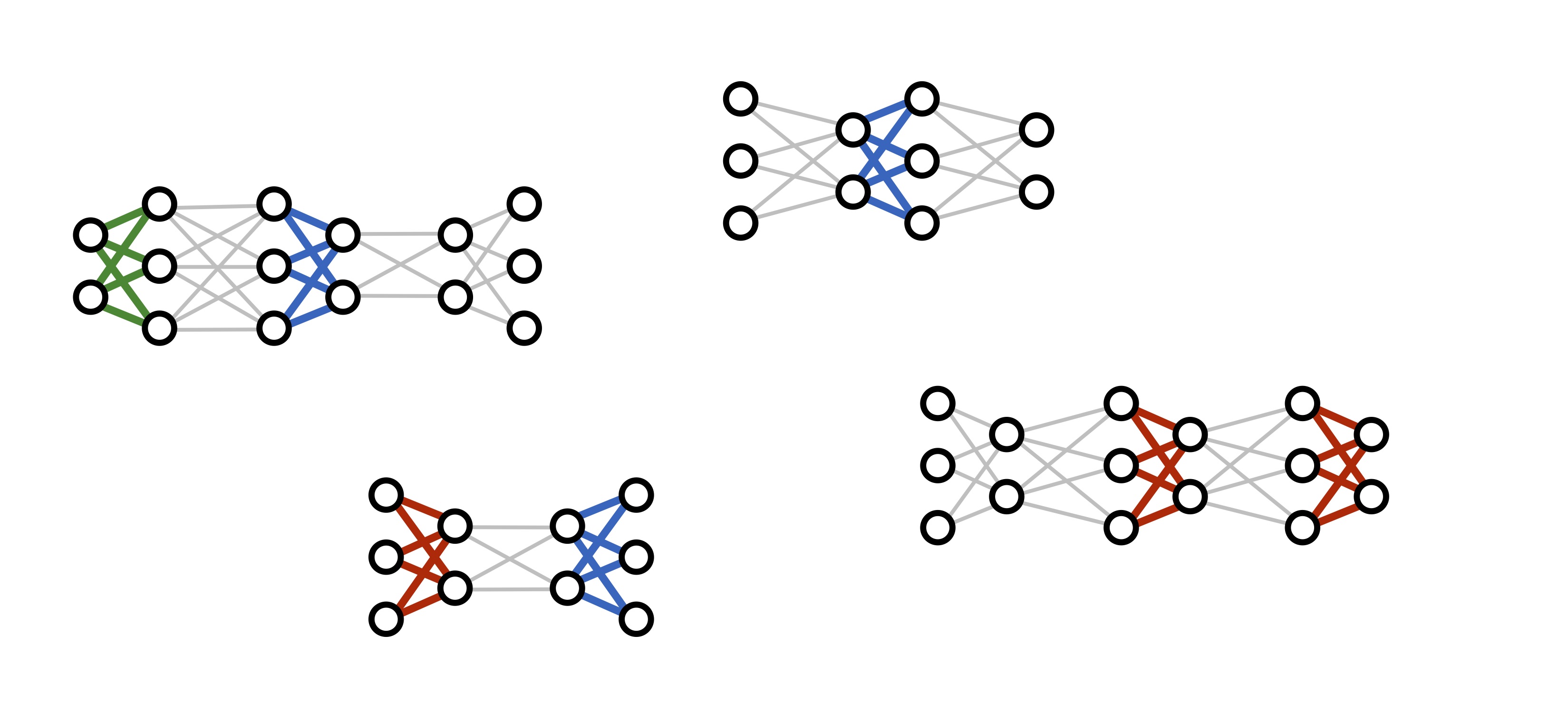
(Several recent deep learning frameworks, including DyNet and TensorFlow Fold, were explicitly designed with this kind of dynamic computation in mind.)

What we get at the end of the training process is not a single deep network, but rather a collection of neural "modules", each of which implements a single step of reasoning. When we want to use our trained model on a new problem instance, we can assemble these modules dynamically to produce a new network structure tailored to that problem.

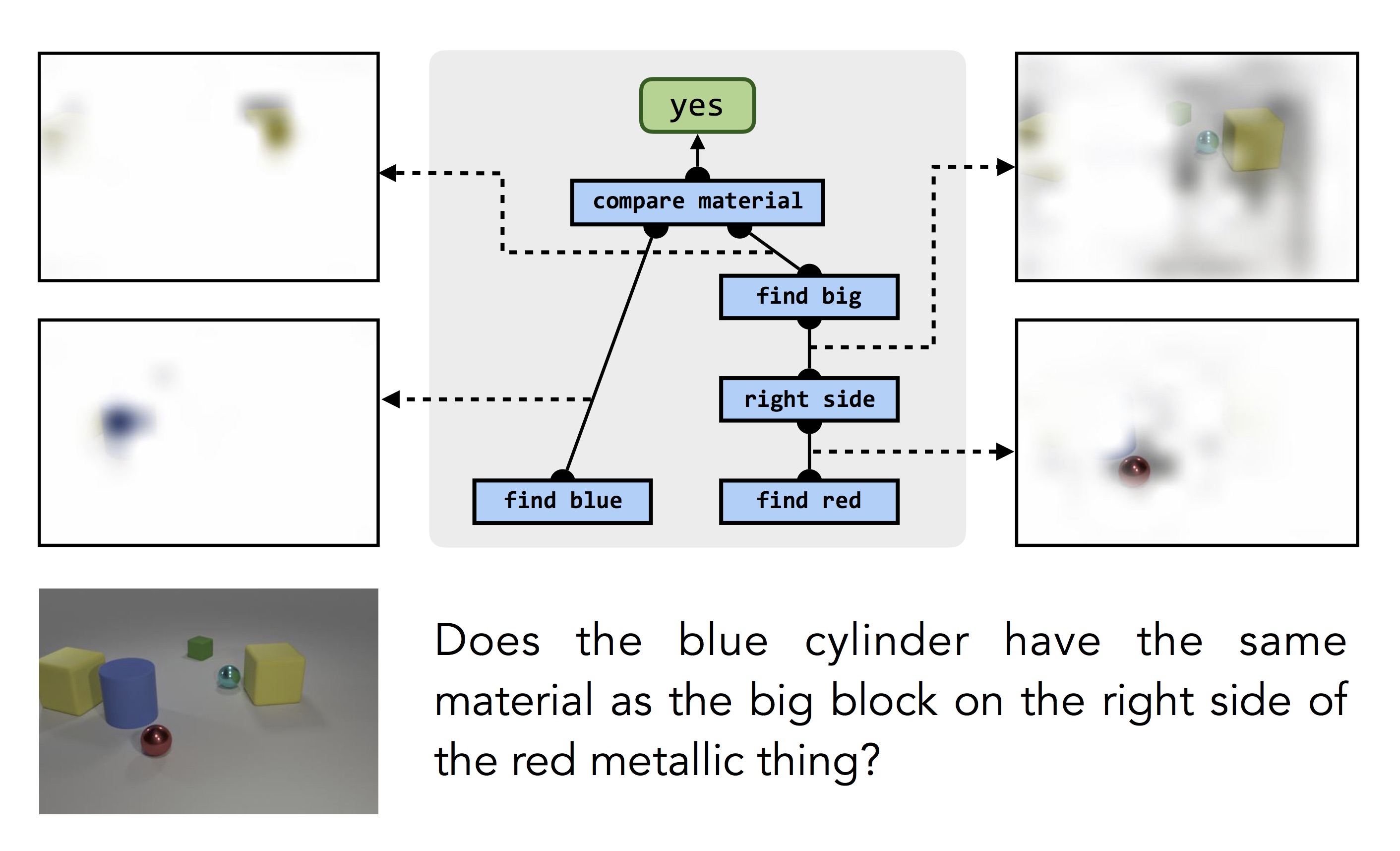
One of the remarkable things about this process is that we don’t need to provide any low-level supervision for individual modules: the model never sees an isolated example of blue object or a "left-of" relationship. Modules are learned only inside larger composed structures, with only (question, answer) pairs as supervision. But the training procedure is able to automatically infer the correct relationship between pieces of structure and the computations they’re responsible for:

This same process works for answering questions about more realistic photographs, and even other knowledge sources like databases:

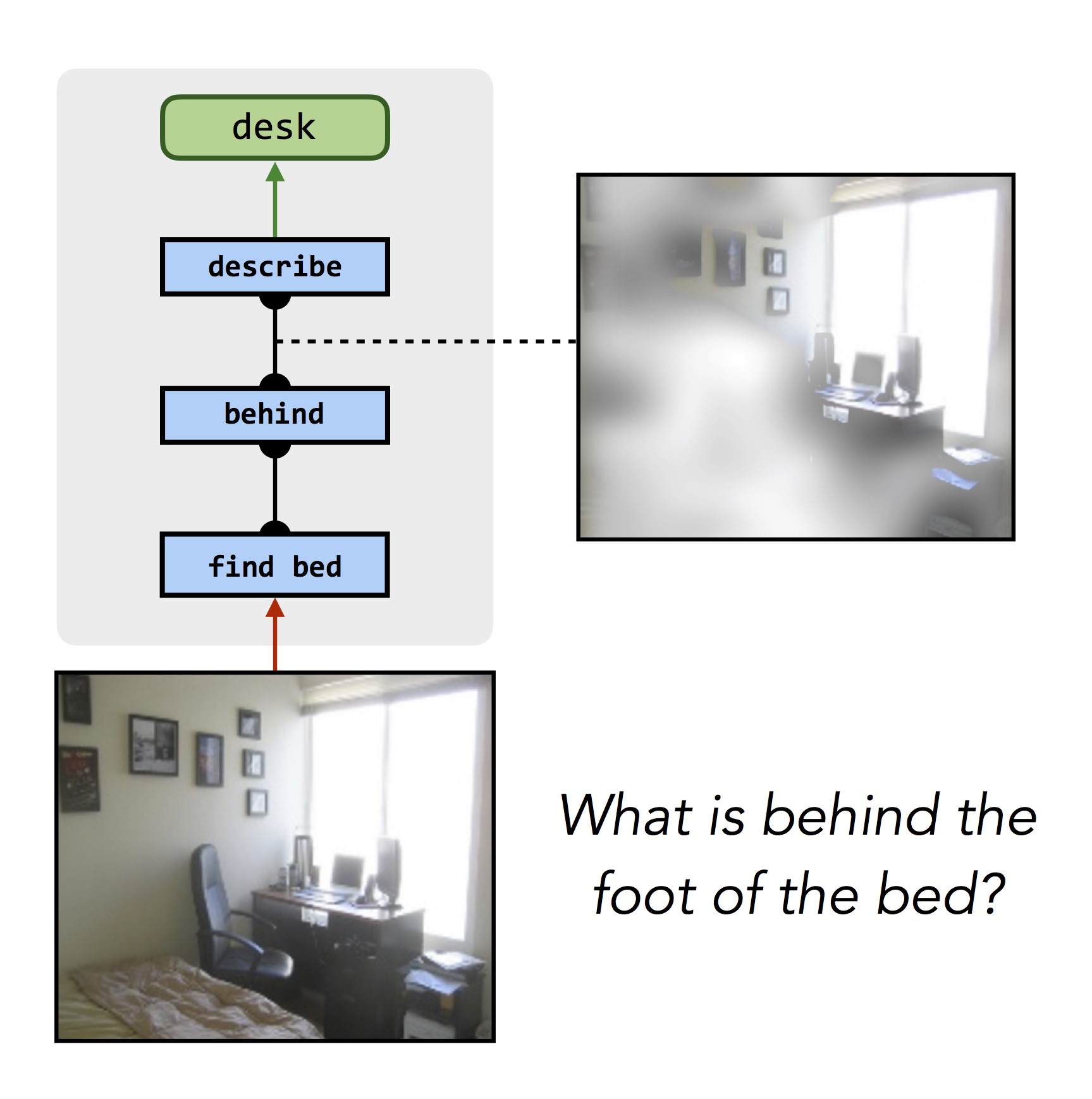
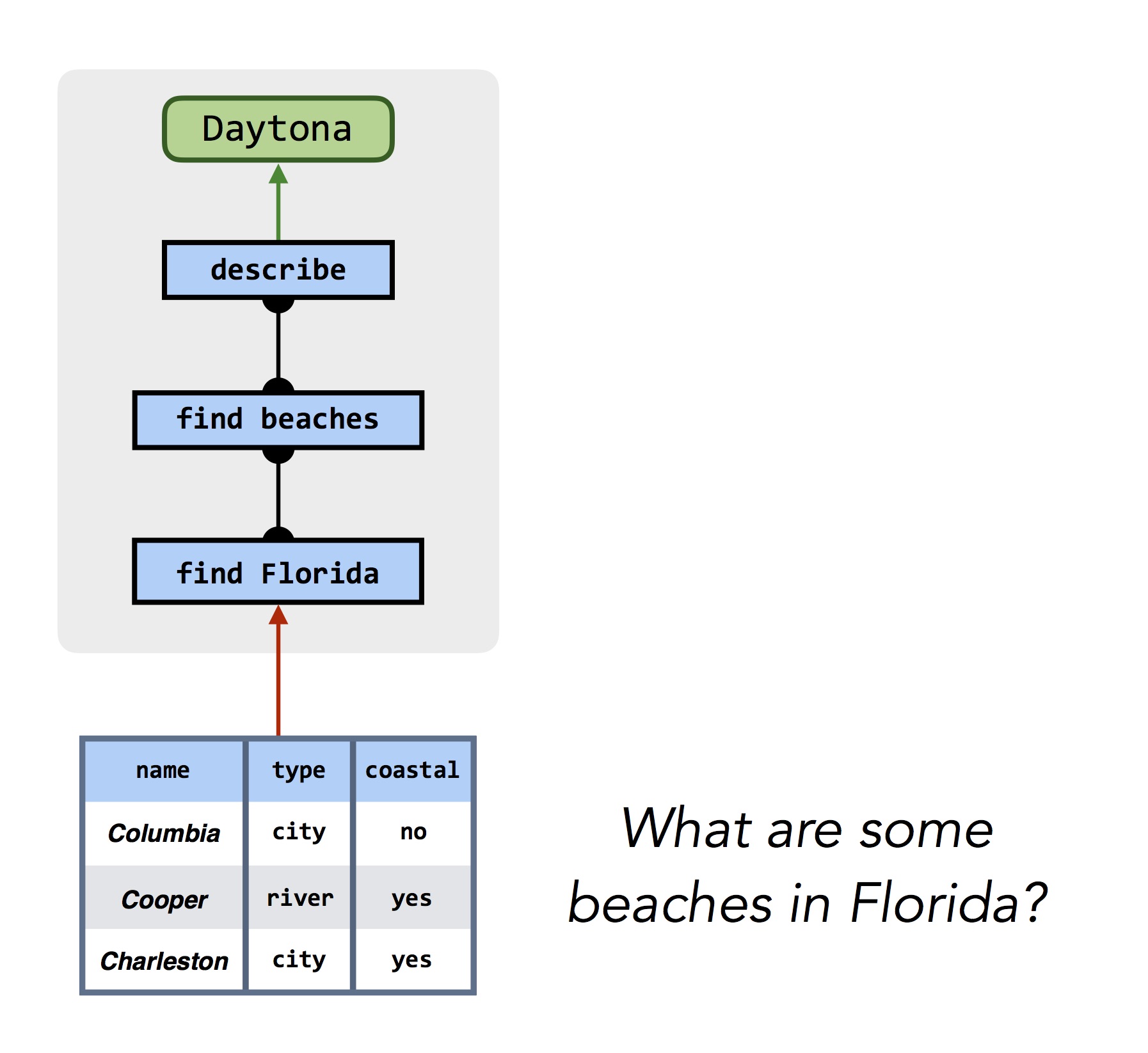
The key ingredient in this whole process is a collection of high-level "reasoning blueprints" like the ones above. These blueprints tell us how the network for each question should be laid out, and how different questions relate to one another. But where do the blueprints come from?

In our initial work on these models (1, 2), we drew on a surprising connection between the problem of designing question-specific neural networks and the problem of analyzing grammatical structure. Linguists have long observed that the grammar of a question is closely related to the sequence of computational steps needed to answer it. Thanks to recent advances in natural language processing, we can use off-the-shelf tools for grammatical analysis to provide approximate versions of these blueprints automatically.

But finding exactly the right mapping from linguistic structure to network structure is still a challenging problem, and the conversion process is prone to errors. In later work, rather than relying on this kind of linguistic analysis, we instead turned to data produced by human experts who directly labeled a collection of questions with idealized reasoning blueprints (3). By learning to imitate these humans, our model was able to improve the quality of its predictions substantially. Most surprisingly, when we took a model trained to imitate experts, but allowed it to explore its own modifications to these expert predictions, it was able to find even better solutions than experts on a variety of questions.

Despite the remarkable success of deep learning methods in recent years, many problems—including few-shot learning and complex reasoning—remain a challenge. But these are exactly the sorts of problems where more structured classical techniques like semantic parsing and program induction really shine. Neural module networks give us the best of both worlds: the flexibility and data efficiency of discrete compositionality, combined with the representational power of deep networks. NMNs have already seen a number of successes for visual and textual reasoning tasks, and we’re excited to start applying them to other AI problems as well.

This post is based on the following papers:

1. Neural Module Networks. Jacob Andreas, Marcus Rohrbach, Trevor Darrell and Dan Klein. CVPR 2016. (arXiv)

2. Learning to Compose Neural Networks for Question Answering. Jacob Andreas, Marcus Rohrbach, Trevor Darrell and Dan Klein. NAACL 2016. (arXiv)

3. Modeling Relationships in Referential Expressions with Compositional Modular Networks. Ronghang Hu, Marcus Rohrbach, Jacob Andreas, Trevor Darrell and Kate Saenko. CVPR 2017. (arXiv)

Images are from the VQA and CLEVR datasets.